题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c,已知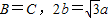 .
.(1)求cosA的值;
(2)
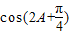 的值.
的值.(3)若已知向量
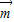 =(
=(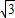 cos
cos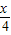 ,cos
,cos ),
),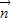 =(sin
=(sin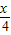 ,cos
,cos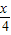 ).若
).若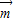 •
•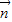 =
=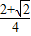 ,求sin(
,求sin(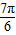 -x)的值.
-x)的值.
【答案】分析:(1)直接利用已知条件以及余弦定理,求cosA的值;
(2)利用(1)的结果,求出sinA,通过二倍角公式求出cos2A,sin2A,利用两角和的余弦函数直接求解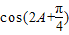 的值.
的值.
(3)通过向量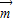 =(
=(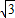 cos
cos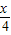 ,cos
,cos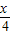 ),
),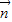 =(sin
=(sin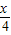 ,cos
,cos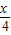 ).利用
).利用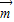 •
•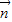 =
=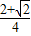 ,求出
,求出 的正弦函数值,利用诱导公式以及二倍角的余弦函数直接求解sin(
的正弦函数值,利用诱导公式以及二倍角的余弦函数直接求解sin(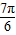 -x)的值.
-x)的值.
解答:解:(1)由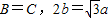 可得c=b=
可得c=b=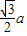 ,
,
所以cosA=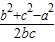 =
=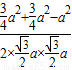 =
= .
.
(2)因为cosA= ,a∈(0,π),所以sinA=
,a∈(0,π),所以sinA=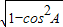 =
=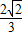 ,
,
cos2A=2cos2A-1=- ,故sin2A=2sinAcosA=
,故sin2A=2sinAcosA=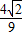 ,
,
∴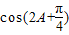 =cos2Acos
=cos2Acos -sin2Asin
-sin2Asin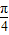 =
=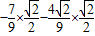 =
=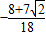 ,
,
(3)向量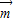 =(
=(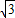 cos
cos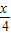 ,cos
,cos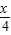 ),
),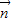 =(sin
=(sin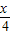 ,cos
,cos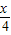 ).
).
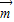 •
•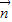 =
=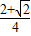 ,(
,(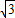 cos
cos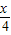 ,cos
,cos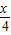 )•(sin
)•(sin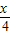 ,cos
,cos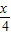 )=
)=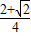 .
.
可得sin(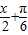 )=
)=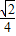 ,
,
sin(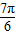 -x)=-cos2(
-x)=-cos2(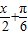 )=2sin2(
)=2sin2( )-1=
)-1= .
.
点评:本题考查余弦定理,同角三角函数的基本关系式,二倍角公式的应用,考查计算能力与转化思想的应用.
(2)利用(1)的结果,求出sinA,通过二倍角公式求出cos2A,sin2A,利用两角和的余弦函数直接求解
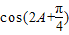 的值.
的值.(3)通过向量
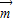 =(
=(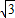 cos
cos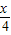 ,cos
,cos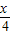 ),
),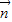 =(sin
=(sin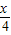 ,cos
,cos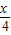 ).利用
).利用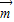 •
•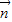 =
=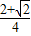 ,求出
,求出 的正弦函数值,利用诱导公式以及二倍角的余弦函数直接求解sin(
的正弦函数值,利用诱导公式以及二倍角的余弦函数直接求解sin(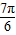 -x)的值.
-x)的值.解答:解:(1)由
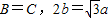 可得c=b=
可得c=b=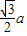 ,
,所以cosA=
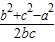 =
=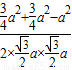 =
= .
.(2)因为cosA=
 ,a∈(0,π),所以sinA=
,a∈(0,π),所以sinA=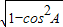 =
=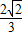 ,
,cos2A=2cos2A-1=-
 ,故sin2A=2sinAcosA=
,故sin2A=2sinAcosA=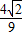 ,
,∴
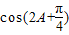 =cos2Acos
=cos2Acos -sin2Asin
-sin2Asin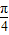 =
=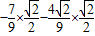 =
=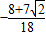 ,
,(3)向量
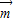 =(
=(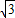 cos
cos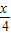 ,cos
,cos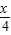 ),
),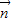 =(sin
=(sin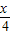 ,cos
,cos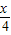 ).
).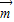 •
•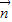 =
=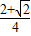 ,(
,(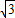 cos
cos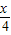 ,cos
,cos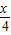 )•(sin
)•(sin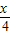 ,cos
,cos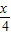 )=
)=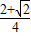 .
.可得sin(
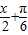 )=
)=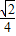 ,
,sin(
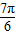 -x)=-cos2(
-x)=-cos2(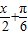 )=2sin2(
)=2sin2( )-1=
)-1= .
.点评:本题考查余弦定理,同角三角函数的基本关系式,二倍角公式的应用,考查计算能力与转化思想的应用.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目