题目内容
求下列双曲线的标准方程：
（1）过点（3，-1），渐近线方程是y=±3x；
（2）与椭圆
+
=1有相同的焦点，且离心率为
．
（1）过点（3，-1），渐近线方程是y=±3x；
（2）与椭圆
| x2 |
| 16 |
| y2 |
| 64 |
| 2 |
根据题意，双曲线的渐近线方程是y=±3x，
设双曲线方程为 9x2-y2=λ（λ≠0），
∵双曲线过点（3，-1），
∴9×9-1=λ，即λ=80．
∴所求双曲线方程为
-
=1；
（2）∵椭圆
+
=1的焦点坐标为（0，4
）和（0，-4
），
根据双曲线的离心率为
．则可设双曲线方程为 y2-x2=a2（a＞0），
∵c=4
，即
a=4
，
∴a=2
．
故所求双曲线方程为
-
=1．
设双曲线方程为 9x2-y2=λ（λ≠0），
∵双曲线过点（3，-1），
∴9×9-1=λ，即λ=80．
∴所求双曲线方程为
| x2 | ||
|
| y2 |
| 80 |
（2）∵椭圆
| x2 |
| 16 |
| y2 |
| 64 |
| 3 |
| 3 |
根据双曲线的离心率为
| 2 |
∵c=4
| 3 |
| 2 |
| 3 |
∴a=2
| 6 |
故所求双曲线方程为
| y2 |
| 24 |
| x2 |
| 24 |
练习册系列答案
相关题目
，一个过点
的双曲线的长轴的端点为椭圆的焦点，求双曲线的标准方程。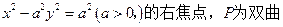
线右支上的一点，
（ ）