题目内容

若f（x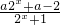）= $数学公式$ 为奇函数，求实数a的值．

解：由题意知，函数的定义域是R，
∵f（x）为奇函数，∴f（x）=-f（-x），
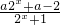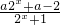即 $\text{[math]}$ =- $\text{[math]}$ ，
∴ $\text{[math]}$ =- $\text{[math]}$ ，
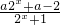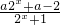∴a=-（a-2），
解得a=1．
分析：根据题意求出函数的定义域是R，再由f（x）=-f（-x）列出方程，整理后利用对应项的系数相等，求出a的值．
点评：本题的考点是利用函数奇偶性求值，即利用奇（偶）函数的定义列出方程，化简后由对应项的系数相等求出参数的值．

练习册系列答案

欢乐假期暑假作业河北美术出版社系列答案

假期冲浪暑假作业东北师范大学出版社系列答案

假期学苑四川教育出版社系列答案

期末复习加暑假作业延边教育出版社系列答案

乐享假期暑假作业延边教育出版社系列答案

仁爱英语开心暑假科学普及出版社系列答案

仁爱英语同步听力训练系列答案

仁爱英语同步学案系列答案

仁爱英语同步整合方案系列答案

仁爱英语同步活页AB卷系列答案

相关题目

设函数f（x）=x|x-a|+b．
（1）当a=1，b=1时，求所有使f（x）=x成立的x的值．
（2）若f（x）为奇函数，求证：a²+b²=0；
（3）设常数b＜2

-3，且对任意x∈[0，1]，f（x）＜0恒成立，求实数a的取值范围．

已知函数y=f（x），x∈R，有下列4个命题：
①若f（1+2x）=f（1-2x），则f（x）的图象关于直线x=1对称；
②f（x-2）与f（2-x）的图象关于直线x=2对称；
③若f（x）为偶函数，且f（2+x）=-f（x），则f（x）的图象关于直线x=2对称；
④若f（x）为奇函数，且f（x）=f（-x-2），则f（x）的图象关于直线x=1对称．
其中正确的命题为

已知f（x）是定义域为R的函数，给出下列命题：
①若f′（1）=0，则x=1是f（x）的极值点；
②若1＜a＜3，则函数f（x）=

(3-a)x-3，x≤7

是单调函数；
③若f（x）为奇函数，又f（x+1）为偶函数，则f（1）+f（3）+…+f（19）=f（2）+f（4）+…+f（20）；
④若f（x）=xⁿ⁺¹（n∈N^*），且f（x）在x=1处的切线与x轴交于点（x_n，0），则lgx₁+lgx₂+…+lgx₉₉=-2
其中正确命题的序号是

（写出所有正确命题的序号）．

已知函数f(x)=a-

．（a∈R）
（1）求证：f（x）是增函数；
（2）若f（x）为奇函数，求实数a的值．．

（2012•安徽模拟）已知函数f(x)=

(a∈R)．
（I）若a=2，且f(x)=-

，求x的值；
（II）若f（x）为奇函数，求a的值；
（III）当a=5时，函数f（x）的图象是否存在对称中心，若存在，求其对称中心；若不存在，请说明理由．