题目内容
15.现有4名同学去参加校学生会活动,共有甲、乙两类活动可供参加者选择,为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪类活动,掷出点数为1或2的人去参加甲类活动,掷出点数大于2的人去参加乙类活动.(1)求这4个人中恰有2人去参加甲类活动的概率;
(2)用X,Y分别表示这4个人中去参加甲、乙两类活动的人数.记ξ=|X-Y|,求随机变量ξ的分布列与数学期望E(ξ).
分析 (1)依题意,这4个人中,每个人去参加甲游戏的概率为$\frac{1}{3}$,去参加乙游戏的人数的概率为$\frac{2}{3}$.设“这4个人中恰有i人去参加甲游戏”为事件Ai(i=0,1,2,3,4),故P(Ai)=${C}_{4}^{i}$($\frac{1}{3}$)i($\frac{2}{3}$)4-i.由此能求出这4个人中恰有2人去参加甲游戏的概率.
(2)ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,求出相应的概率,可得ξ的分布列与数学期望.
解答 解:(1)依题意,这4个人中,每个人去参加甲游戏的概率为$\frac{1}{3}$,去参加乙游戏的人数的概率为$\frac{2}{3}$.
设“这4个人中恰有i人去参加甲游戏”为事件Ai(i=0,1,2,3,4),故P(Ai)=${C}_{4}^{i}$($\frac{1}{3}$)i($\frac{2}{3}$)4-i.
∴这4个人中恰有2人去参加甲游戏的概率为P(A2)=${C}_{4}^{2}(\frac{1}{3})^{2}(\frac{2}{3})^{2}=\frac{8}{27}$.
(2)ξ的所有可能取值为0,2,4,由于A1与A3互斥,A0与A4互斥,
故P(ξ=0)=P(A2)=$\frac{8}{27}$,
P(ξ=2)=P(A1)+P(A3)=$\frac{40}{81}$,
P(ξ=4)=P(A0)+P(A4)=$\frac{17}{81}$,
∴ξ的分布列是:
| ξ | 0 | 2 | 4 |
| P | $\frac{8}{27}$ | $\frac{40}{81}$ | $\frac{17}{81}$ |
点评 本题考查概率知识的求解,考查互斥事件的概率公式,考查离散型随机变量的分布列与期望,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
7.已知2sinθ=1-cosθ,则tanθ=( )
| A. | -$\frac{4}{3}$或0 | B. | $\frac{4}{3}$或0 | C. | -$\frac{4}{3}$ | D. | $\frac{4}{3}$ |
7.集合A={-1,0,1,2,3},B={x|log2(x+1)<2},则A∩B等于( )
| A. | {-1,0,1,2} | B. | {0,1,2} | C. | {-1,0,1,2,3} | D. | {0,1,2,3} |
3.已知集合A={x|x2-x-2<0},B={y|y=ex,x<ln3},则A∪B=( )
| A. | (-1,3) | B. | (-1,0) | C. | (0,2) | D. | (2,3) |
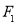 、
、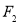 是双曲线
是双曲线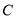 :
: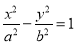 (
(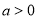 ,
,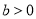 )的左、右焦点,
)的左、右焦点,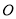 为坐标原点,点
为坐标原点,点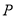 在双曲线
在双曲线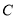 的右支上,且满足
的右支上,且满足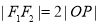 ,
,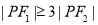 ,则双曲线
,则双曲线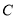 的离心率的取值范围为( )
的离心率的取值范围为( )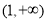 B.
B.
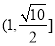 D.
D.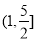
 的图像大致是( )
的图像大致是( )
 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.