题目内容
10．函数f（x）=ex+x2-4的一个零点所在区间为（ ）| A． | （-3，-2） | B． | （-1，0） | C． | （0，1） | D． | （1，2） |
分析 由函数的解析式求得f（1）f（2）＜0，再根据根据函数零点的判定定理可得函数f（x）=ex+x2-4的零点所在的区间．
解答 解：∵函数f（x）=ex+x2-4，
∴f（1）=e+1-4=e-3＜0，f（2）=e2+4-4＞0，
∴f（1）f（2）＜0．
根据函数零点的判定定理可得函数f（x）=ex+x2-4的零点所在的区间是（1，2），
故选：D．
点评 本题主要考查求函数的值，函数零点的判定定理，属于基础题．
练习册系列答案
相关题目
20．
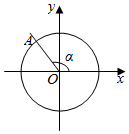如图所示，在平面直角坐标系xOy中，角α的终边与单位圆交于点A．若点A的纵坐标是$\frac{4}{5}$，那么sinα的值是（ ）
如图所示，在平面直角坐标系xOy中，角α的终边与单位圆交于点A．若点A的纵坐标是$\frac{4}{5}$，那么sinα的值是（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
1．与sin2016°最接近的数是（ ）
| A． | $\frac{11}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | -1 |
5．已知下表所示数据的回归直线方程为$\stackrel{∧}{y}$=-1.3x+a，则实数a=19.2．
| X | 2 | 3 | 4 | 5 | 6 |
| Y | 11 | 13 | 14 | 16 | 16 |