题目内容
已知椭圆C:
+
=1.
(1)双曲线与椭圆C具有相同的焦点,且它们的离心率互为倒数,求双曲线的方程;
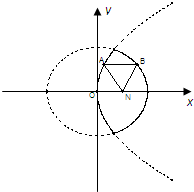
(2)设椭圆C的右焦点为F2,A、B是椭圆上的点,且
=2
,求直线AB的斜率.
| x2 |
| 4 |
| y2 |
| 3 |
(1)双曲线与椭圆C具有相同的焦点,且它们的离心率互为倒数,求双曲线的方程;
(2)设椭圆C的右焦点为F2,A、B是椭圆上的点,且
| AF2 |
| F2B |
(1)由已知,椭圆的焦点坐标为(-1,0),(1,0),离心率为
,
所以所求双曲线焦点坐标为(-1,0),(1,0),离心率为2,…(2分)
双曲线c=1,
=2,解得a2=
,b2=
,
所求双曲线方程为4x2-
=1.…(4分)
(2)设A(x1,y1),由
=2
得B(
,-
),…(5分)
由A,B两点在椭圆上,得
+
=1,
+
=4,…(8分)
解得x1=-
,y1=±
,…(10分)
所以k=
=±
.…(12分)
| 1 |
| 2 |
所以所求双曲线焦点坐标为(-1,0),(1,0),离心率为2,…(2分)
双曲线c=1,
| c |
| a |
| 1 |
| 4 |
| 3 |
| 4 |
所求双曲线方程为4x2-
| 4y2 |
| 3 |
(2)设A(x1,y1),由
| AF2 |
| F2B |
| 3-x1 |
| 2 |
| y1 |
| 2 |
由A,B两点在椭圆上,得
| x12 |
| 4 |
| y12 |
| 3 |
| (3-x1)2 |
| 4 |
| y12 |
| 3 |
解得x1=-
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
所以k=
| y1 |
| x1-1 |
| ||
| 2 |

练习册系列答案
相关题目