题目内容
设OABC是四面体,G1是△ABC的重心,G是OG1上一点,且OG=3GG1,若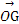 =x
=x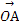 +y
+y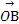 +z
+z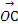 ,则(x,y,z)为( )
,则(x,y,z)为( )
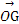 =x
=x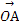 +y
+y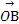 +z
+z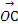 ,则(x,y,z)为( )
,则(x,y,z)为( )A.( , , , , ) ) | B.( , , , , ) ) |
C.( , , , , ) ) | D.( , , , , ) ) |
A
 =
=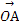 +
+
=
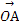 +
+ ×
× (
( +
+ )
)=
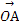 +
+ [(
[(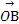 -
-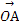 )+(
)+(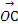 -
-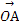 )]
)]=
 (
(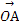 +
+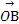 +
+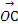 ),
),由OG=3GG1知,
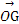 =
= =
= (
(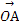 +
+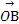 +
+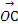 ),
),∴(x,y,z)=(
 ,
, ,
, ).
).
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
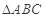 中,
中,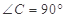 ,
, D、E分别是
D、E分别是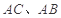 上的点,且
上的点,且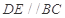 ,将
,将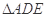 沿
沿 折起到
折起到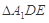 的位置,使
的位置,使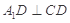 ,如图2.
,如图2.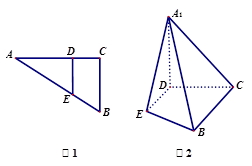
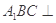 平面
平面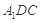 ;
;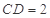 ,求
,求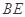 与平面
与平面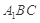 所成角的余弦值;
所成角的余弦值;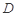 点在何处时,
点在何处时,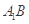 的长度最小,并求出最小值.
的长度最小,并求出最小值.

 中,
中,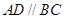 ,
,
 ,
, ,如图,把
,如图,把 沿
沿 翻折,使得平面
翻折,使得平面 平面
平面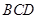 .
.


 ;
;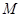 为线段
为线段 中点,求点
中点,求点 的距离;
的距离; ,使得
,使得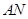 与平面
与平面 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.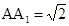 ,点E、F分别是面A1C1、面BC1的中心.
,点E、F分别是面A1C1、面BC1的中心.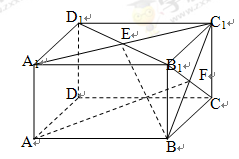
 =(1,5,-2),
=(1,5,-2),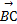 =(3,1,z),若
=(3,1,z),若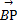 =(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为( )
=(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为( )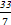 ,-
,-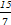 ,4
,4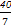 ,-
,-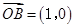 ,
,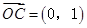 ,A为动点,
,A为动点,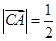 ,则
,则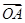 与
与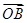 夹角的最小值为( )
夹角的最小值为( )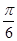
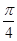
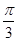
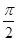
 )平行,则λ=( )
)平行,则λ=( )
