题目内容
11.已知k∈Z,$\overrightarrow{AB}$=(k,1),$\overrightarrow{AC}$=(2,4),若|$\overrightarrow{AB}$|≤$\sqrt{17}$,则∠B是直角的概率是( )| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
分析 根据向量模长公式求出满足条件的k的个数,再根据古典概型的计算公式进行求解.
解答 解:由丨$\overrightarrow{AB}$丨≤$\sqrt{17}$,k∈Z知,
k2+1≤17,
∴k∈{-4,-3,-2,-1,0,1,2,3,4},
由$\overrightarrow{AB}$=(k,1),$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$=(2-k,3),且$\overrightarrow{AB}$⊥$\overrightarrow{BC}$,
∴$\overrightarrow{AB}$•$\overrightarrow{BC}$=k(2-k)+3=0,
解得k=-1,3,
∴∠ABC是直角的概率为P=$\frac{2}{9}$.
故选:C.
点评 本题主要考查了概率的计算,根据古典概型的概率公式进行计算即可.

练习册系列答案
相关题目
1.已知a=lg3,$b={4^{\frac{1}{3}}}$,c=lg0.3,这三个数的大小关系为( )
| A. | b<a<c | B. | a<b<c | C. | c<a<b | D. | c<b<a |
2.在公差d=3的等差数列{an}中,a2+a4=-2,则数列{|an|}的前10项和为( )
| A. | 127 | B. | 125 | C. | 89 | D. | 70 |
6.函数f(x)=$\sqrt{x+1}+\frac{1}{x}$的定义域为( )
| A. | [-1,0)∪(0,+∞) | B. | (-1,0)∪(0,+∞) | C. | [-1,+∞) | D. | (0,+∞) |
3.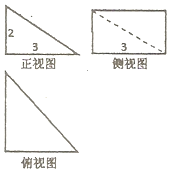 已知一几何体的正视图、俯视图为直角三角形,侧视图为矩形,则该几何体的体积为( )
已知一几何体的正视图、俯视图为直角三角形,侧视图为矩形,则该几何体的体积为( )
 已知一几何体的正视图、俯视图为直角三角形,侧视图为矩形,则该几何体的体积为( )
已知一几何体的正视图、俯视图为直角三角形,侧视图为矩形,则该几何体的体积为( )| A. | 6 | B. | 12 | C. | 18 | D. | 36 |
20.双曲线的渐近线方程为y=±4x,则该双曲线的离心率为( )
| A. | 5 | B. | $\sqrt{5}$ | C. | $\sqrt{17}$或$\frac{\sqrt{17}}{4}$ | D. | $\sqrt{17}$或$\frac{\sqrt{17}}{2}$ |
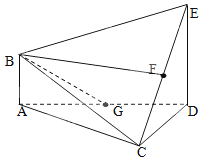 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点,F是CE的中点.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点,F是CE的中点.