题目内容
20.设Sn是数列{an}的前n项和,已知${a_1}≠0,3{a_n}-{a_1}={S_1}{S_n},n∈{N^*}$.(1)求a1,并求数列{an}的通项公式;
(2)求数列$\left\{{\frac{{n{a_n}}}{2}}\right\}$的前项和Tn.
分析 (1)${a_1}≠0,3{a_n}-{a_1}={S_1}{S_n},n∈{N^*}$.n=1时,3a1-${a}_{1}={a}_{1}^{2}$,解得a1=2.Sn=$\frac{1}{2}(3{a}_{n}-2)$,n≥2时,an=Sn-Sn-1,化为an=3an-1,利用等比数列的通项公式即可得出.${a}_{n}=2×{3}^{n-1}$.
(2)由(1)可知:$\frac{n{a}_{n}}{2}$=n•3n-1.利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)∵${a_1}≠0,3{a_n}-{a_1}={S_1}{S_n},n∈{N^*}$.
∴n=1时,3a1-${a}_{1}={a}_{1}^{2}$,解得a1=2.
∴Sn=$\frac{1}{2}(3{a}_{n}-2)$,n≥2时,an=Sn-Sn-1=$\frac{1}{2}(3{a}_{n}-2)$-$\frac{1}{2}(3{a}_{n-1}-2)$,
化为an=3an-1,
∴${a}_{n}=2×{3}^{n-1}$.
(2)由(1)可知:$\frac{n{a}_{n}}{2}$=n•3n-1.
∴数列$\left\{{\frac{{n{a_n}}}{2}}\right\}$的前项和Tn=1+2×3+3×32+…+n•3n-1,
3Tn=3+2×32+…+(n-1)•3n-1+n•3n,
∴-2Tn=1+3+32+…+3n-1-n•3n=$\frac{{3}^{n}-1}{3-1}$-n•3n,
∴Tn=$\frac{(2n-1)•{3}^{n}+1}{4}$.
点评 本题考查了等比数列的通项公式与求和公式、“错位相减法”、数列递推关系,考查了推理能力与计算能力,属于中档题.

| A. | $[2kπ-\frac{π}{4},2kπ+\frac{π}{4})\begin{array}{l}{\;}&{(k∈Z)}\end{array}$ | B. | $[2kπ-\frac{5π}{4},2kπ-\frac{π}{4}]\begin{array}{l}{\;}&{(k∈Z)}\end{array}$ | ||
| C. | $[2kπ-\frac{π}{4},2kπ+\frac{3π}{4}]\begin{array}{l}{\;}&{(k∈Z)}\end{array}$ | D. | $(2kπ-\frac{3π}{4},2kπ-\frac{π}{4}]\begin{array}{l}{\;}&{(k∈Z)}\end{array}$ |
| A. | x+y=0 | B. | x-y=0 | C. | x-y+1=0 | D. | x+y-1=0 |
| A. | 3 | B. | ${log_3}\frac{1}{2}$ | C. | log32 | D. | $\sqrt{3}$ |
| A. | 25π | B. | 200π | C. | 100π | D. | 50π |
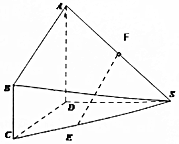 如图,在几何体SABCD中,AD⊥平面SCD,BC∥AD,AD=DC=2,BC=1,又SD=2,∠SDC=120°,F是SA的中点,E在SC上,AE=$\sqrt{5}$.
如图,在几何体SABCD中,AD⊥平面SCD,BC∥AD,AD=DC=2,BC=1,又SD=2,∠SDC=120°,F是SA的中点,E在SC上,AE=$\sqrt{5}$.