题目内容
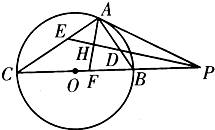如图，直线PA与圆O相切于点A，PBC是过点O的割线，∠APE=∠CPE，点H是线段ED的中点．（1）证明：A，E，F，D四点共圆；
（2）证明：PF2=PB•PC．
考点：与圆有关的比例线段
专题：推理和证明
分析：（1）连接EF，证明EF∥AB，再证明∠AFE=∠ADE，即可证明A，E，F，D四点共圆．
（2）由AF平分∠CAB，得∠CAF=∠BAF，由弦切角定理得∠PAB=∠ACB，从而∠PFA=∠PAF，由此能证明PF2=PA2=PB•PC．
（2）由AF平分∠CAB，得∠CAF=∠BAF，由弦切角定理得∠PAB=∠ACB，从而∠PFA=∠PAF，由此能证明PF2=PA2=PB•PC．
解答：
证明：（1）连接EF，则
∵直线PA与圆O相切于点A，PBC是过点O的割线，∠APC的角平分线交AC于点E，
∴∠PAB=∠PCA，∠APE=∠CPE，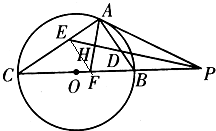
∴∠ADP=∠PEC，△PAC∽△PBA，
∴∠AED=∠ADE，
=
，
∵点H是线段ED的中点，∴AF平分∠CAB，∴
=
，
∵∠APC的角平分线交AC于点E，
=
，∴
=
，
∴EF∥AB，∵AB⊥AC，∴EF⊥AC，∴∠AEH=∠AFE，
∴∠AFE=∠ADE，∴A，E，F，D四点共圆．
（2）∵AF平分∠CAB，∴∠CAF=∠BAF，
∵AP是切线，∴∠PAB=∠ACB，
∴∠PFA=∠PAF，∴PA=PF，
∴PF2=PA2=PB•PC．
∵直线PA与圆O相切于点A，PBC是过点O的割线，∠APC的角平分线交AC于点E，
∴∠PAB=∠PCA，∠APE=∠CPE，
∴∠ADP=∠PEC，△PAC∽△PBA，
∴∠AED=∠ADE，
| AC |
| AB |
| PC |
| PA |
∵点H是线段ED的中点，∴AF平分∠CAB，∴
| CF |
| FB |
| AC |
| AB |
∵∠APC的角平分线交AC于点E，
| CE |
| EA |
| PC |
| PA |
| CE |
| EA |
| CF |
| FB |
∴EF∥AB，∵AB⊥AC，∴EF⊥AC，∴∠AEH=∠AFE，
∴∠AFE=∠ADE，∴A，E，F，D四点共圆．
（2）∵AF平分∠CAB，∴∠CAF=∠BAF，
∵AP是切线，∴∠PAB=∠ACB，
∴∠PFA=∠PAF，∴PA=PF，
∴PF2=PA2=PB•PC．
点评：本小题主要考查与圆有关的比例线段、四点共圆的证明方法、三角形相似、弦切角定理、切割线定理等基础知识，考查运算求解能力、化归与转化思想．属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
设
，
为向量，若
+
与
的夹角为60°，
+
与
的夹角为45°，则
=（ ）
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
|
| ||
|
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个空间几何体的三视图如图所示，其中正视图为等腰直角三角形，侧视图与俯视图为正方形，则该几何体的体积为