题目内容
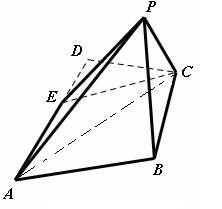
(本小题13分)如图1,在三棱锥P—ABC中, 平面ABC,
平面ABC,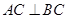 ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。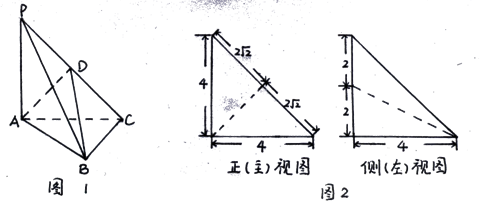
(1)证明: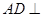 平面PBC;
平面PBC;
(2)求三棱锥D—ABC的体积;
(3)在 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得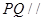 平面ABD,并求此时PQ的长。
平面ABD,并求此时PQ的长。
(1)根据已知题意,可知 ,然后结合
,然后结合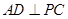 来得到证明。
来得到证明。
(2)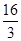 (3)
(3)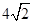
解析试题分析:(1)由主视图可知D为PC中点,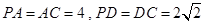
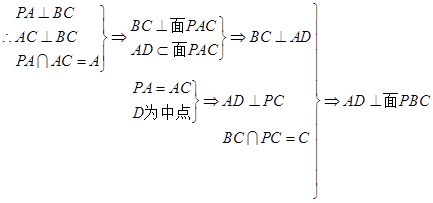
(2)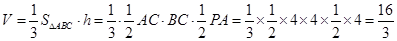
(3)设 的角平分线交AB于M,连DM,CM并延长CM至
的角平分线交AB于M,连DM,CM并延长CM至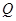 ,使得
,使得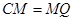 ,连接
,连接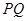

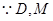 分别是
分别是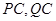 的中点,
的中点,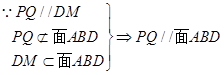
又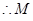 为AB、CQ中点
为AB、CQ中点
∴四边形ACBQ为正方形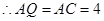
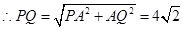
考点:空间中的点线面位置关系以及体积
点评:解决的关键是对于线面垂直的判定定理和性质定理的运用,属于基础题。

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
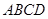 中,
中,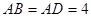 ,
,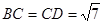 ,点
,点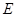 为线段
为线段 上的一点.现将
上的一点.现将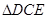 沿线段
沿线段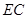 翻折到
翻折到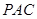 (点
(点 与点
与点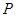 重合),使得平面
重合),使得平面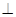 平面
平面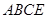 ,连接
,连接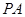 ,
,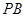 .
.
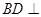 平面
平面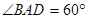 ,且点
,且点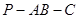 的大小.
的大小.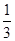 BB1,C1F=
BB1,C1F=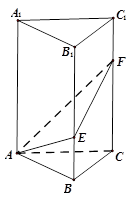
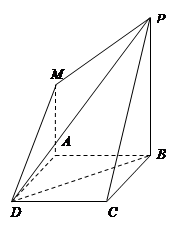
 中,
中, ,且E、F分别是AB、BD的中点,
,且E、F分别是AB、BD的中点,
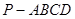 中,
中, 底面
底面 ,
,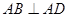 ,
,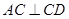 ,
,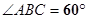 ,
,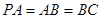 ,
,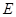 是
是 的中点.
的中点.
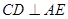 ;
; 平面
平面 ;
; 的余弦值.
的余弦值.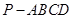 中
中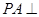 平面
平面 ,
,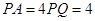 ,底面为直角梯形,
,底面为直角梯形,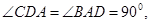
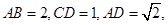
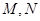 分别是
分别是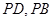 的中点.
的中点.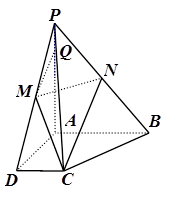
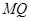 // 平面
// 平面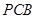 ;
;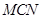 与底面
与底面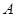 到平面
到平面