题目内容
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=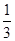 BB1,C1F=
BB1,C1F=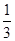 CC1.
CC1.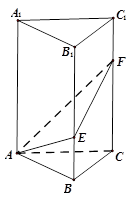
(1)求异面直线AE与A1 F所成角的大小;
(2)求平面AEF与平面ABC所成角的余弦值.
(1)60º.(2)
解析试题分析:解:(1)建立如图所示的直角坐标系,则
 ,
, ,
, ,
, ,从而
,从而 ,
, . 2分
. 2分
记 与
与 的夹角为
的夹角为 ,则有
,则有 .
.
又由异面直线 与
与 所成角的范围为
所成角的范围为 ,可得异面直线
,可得异面直线 与
与 所成的角为60º. 4分
所成的角为60º. 4分
(2)记平面 和平面
和平面 的法向量分别为n和m,则由题设可令
的法向量分别为n和m,则由题设可令 ,且有平面
,且有平面 的法向量为
的法向量为 ,
,  ,
, .
.
由 ,得
,得 ;由
;由 ,得
,得 .
.
所以 ,即
,即 . 8分
. 8分
记平面 与平面
与平面 所成的角为
所成的角为 ,有
,有 .
.
由题意可知 为锐角,所以
为锐角,所以 . 10分
. 10分
考点:异面直线所成的角,二面角的平面角
点评:对于角的求解,一般先左后证,三解答,异面直线的所成的角一般平移法得到,对于二面角的求解,通常运用向量法,合理的建系是关键,属于基础题。

练习册系列答案
相关题目
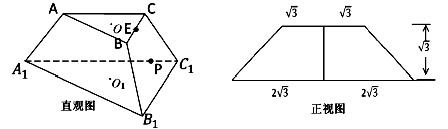
 的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,
的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱, ,
,
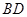 与B1E所成角的大小;
与B1E所成角的大小;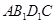 的体积.
的体积.  ,如图二,在二面角
,如图二,在二面角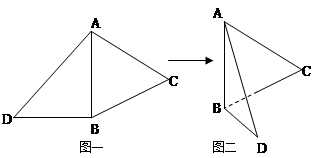
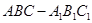 中,
中, ,
,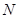 是
是 的中点,
的中点,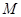 是线段
是线段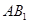 上的动点(与端点不重合),且
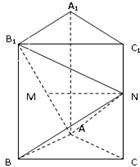
上的动点(与端点不重合),且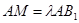 .
.
 ,求证:
,求证: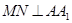 ;
; 与平面
与平面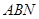 所成角的大小为
所成角的大小为 ,求
,求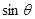 的最大值.
的最大值.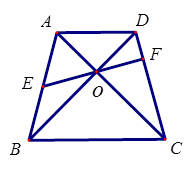
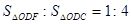
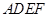 与梯形
与梯形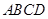 所在的平面互相垂直,
所在的平面互相垂直,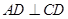 ,
, ∥
∥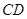 ,
,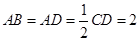 ,点
,点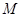 在线段
在线段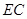 上.
上.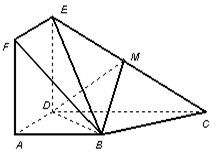
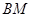 ∥平面
∥平面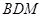 与平面
与平面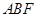 所成锐二面角的余弦值为
所成锐二面角的余弦值为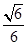 时,求三棱锥
时,求三棱锥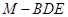 的体积.
的体积. 平面ABC,
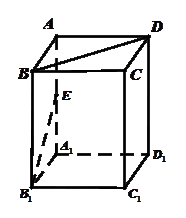
平面ABC,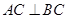 ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。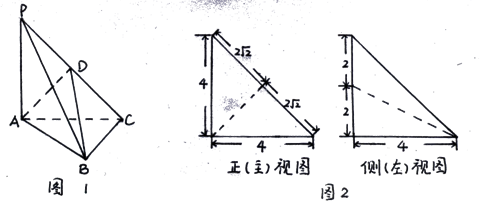
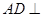 平面PBC;
平面PBC; 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得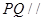 平面ABD,并求此时PQ的长。
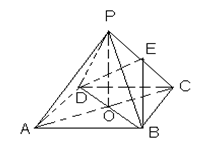
平面ABD,并求此时PQ的长。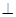 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.