题目内容
解关于x的不等式
解法一:原不等式等价于
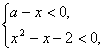
或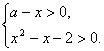
即![]()
或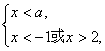
①当a<-1时,不等式解集为
(-∞,a)∪(-1,2);
②当a=-1时,
解集(-∞,-1)∪(-1,2);
③当-1<a<2时,
得x∈(-∞,-1)∪(a,2);
④当a=2时,得x∈(-∞,-1);
⑤当a>2时,得x∈(2,a)∪(-∞,-1).
解法二:原不等式等价于(x-a)(x+1)(x-2)<0.
①当a<-1,由下图知不等式解集为(-∞,a)∪(-1,2);
![]()
②当a=-1,原不等式等价于(x+1)2(x-2)<0![]()
∴解集为(-∞,-1)∪(-1,2);
③当-1<a<2时,由下图知不等式解集为(-∞,-1)∪(a,2);
![]()
④当a=2时,原不等式等价于(x+1)(x-2)2<0![]()
∴解集(-∞,-1);
⑤当a>2时由下图知不等式解集为(-∞,-1)∪(2,a).
![]()
温馨提示
解含参数的不等式时,要适时分类讨论,同时避免重复与遗漏.

练习册系列答案
相关题目
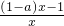 <0.
<0. <0.
<0.