题目内容
(本小题满分12分)
某校共有800名学生,高三一次月考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
| 组号 | 第 一 组 | 第 二 组 | 第 三 组 | 第 四 组 | 第 五 组 | 第 六 组 | 第 七 组 | 第 八 组 | 合计 |
| 分组 | 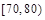 | 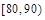 |  | 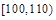 | 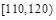 | 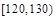 | 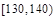 | 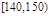 | |
| 频数 | 4 | 6 | 20 | 22 | 18 | 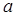 | 10 | 5 | 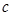 |
| 频率 | 0.04 | 0.06 | 0.20 | 0.22 | 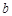 | 0.15 | 0.10 | 0.05 | 1 |
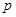 ;
;(Ⅱ)为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生的成绩,并在这6名学生中在随机抽取2名由心理老师张老师负责面谈,求第七组至少有一名学生与张老师面谈的概率;
(Ⅲ)估计该校本次考试的数学平均分。

 (1)
(1) ;
;
(2)抽取2个的方法有ab ac ad aE aF bd bc bE bF cd cE cF dE dF EF, 共15种。
至少含E或F的取法有 9种,概率为;
(3)估计平均分为110.4分。
解析试题分析:因为频率和为1 所以 (1分)
(1分)
因为频率=频数/样本容量 所以 (3分)
(3分)
(1)每位学生成绩被抽取的机会均等  (5分)
(5分)
(2) 在第六、七、八组共有30个样本,用分层抽样方法抽取6名学生的成绩,每个被抽取的概率为 。第七组被抽取的样本数为
。第七组被抽取的样本数为 。
。
将第六组、第八组抽取的样本用a,b,c,d表示,第七组抽出的样本用E,F表示。
抽取2个的方法有ab ac ad aE aF bd bc bE bF cd cE cF dE dF EF, 共15种。
至少含E或F的取法有 9种,概率为 (9分)
(9分)
(3)75x0.04+85x0.06+95x0.2+105x0.22+115x0.18
+125x0.15+135x0.1+145x0.05=110.4 估计平均分为110.4分 (12分)
考点:本题主要考查抽样方法,频率的概念及计算,古典概型概率的计算。
点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案(理科)PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095 – 2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
| PM2.5日均值 (微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
(本题10分) 为了解高二学年女生身高情况,对高二(10)班女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 | 频数 | 频率 |
| 145.5~149.5 | 1 | 0.02 |
| 149.5~153.5 | 4 | 0.08 |
| 153.5~157.5 | 20 | 0.40 |
| 157.5~161.5 | 15 | 0.30 |
| 161.5~165.5 | 8 | 0.16 |
| 165.5~169.5 | m | n |
| 合 计 | M | N |
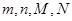 所表示的数分别是多少?
所表示的数分别是多少?(2)若该校高二学年共有女生500人,试估计高二女生中身高在161.5以上的人数。
(本小题满分12分)某公司欲招聘员工,从1000名报名者中筛选200名参加笔试,按笔试成绩择优取50名面试,再从面试对象中聘用20名员工.
(1)求每个报名者能被聘用的概率;
(2)随机调查了24名笔试者的成绩如下表所示:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人数 | 1 | 2 | 6 | 9 | 5 | 1 |
(3)公司从聘用的四男
 、
、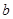 、
、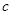 、
、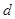 和二女
和二女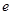 、
、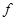 中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
中选派两人参加某项培训,则选派结果为一男一女的概率是多少? 电视传媒公司为了解某地区观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名。下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%的把握认为“体育迷”与性别有关?
| | 非体育迷 | 体育迷 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | |
附:K2=
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(本小题满分10分)国家有甲,乙两个射击队,若两个队共进行了8次热身赛,
各队的总成绩见下表:
| 甲队 | 403 | 390 | 397 | 404 | 388 | 400 | 412 | 406 |
| 乙队 | 417 | 401 | 410 | 416 | 406 | 421 | 398 | 411 |
分别求两个队总成绩的样本平均数和样本方差,根据计算结果,若选一个代表队参加奥运会比赛,你认为应该选哪一个队?
(本小题满分13分)某同学大学毕业后在一家公司上班,工作年限 和年收入
和年收入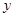 (万元),有以下的统计数据:
(万元),有以下的统计数据:
 | 3 | 4 | 5 | 6 |
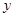 | 2.5 | 3 | 4 | 4.5 |
(Ⅱ)请根据上表提供的数据,用最小二乘法求出
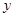 关于
关于 的线性回归方程
的线性回归方程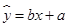 ;
;(Ⅲ)请你估计该同学第8年的年收入约是多少?
(参考公式:
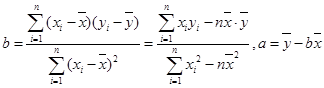 )
)  户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图). 的值,并估计该社区家庭月均用水量不超过
的值,并估计该社区家庭月均用水量不超过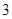 吨的频率;
吨的频率; 、
、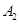 、
、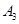 是户月均用水量为
是户月均用水量为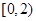 的居民代表,
的居民代表, 、
、 是户月均用水量为
是户月均用水量为 的居民代表. 现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表
的居民代表. 现从这五位居民代表中任选两人参加水价论证会,请列举出所有不同的选法,并求居民代表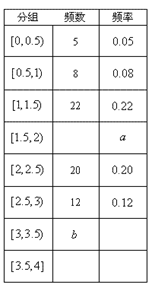
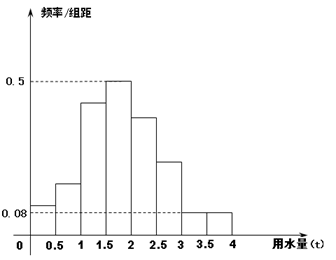
 ,
, ,…,
,…, 后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题: