题目内容
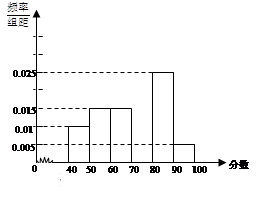
电视传媒公司为了解某地区观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名。下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%的把握认为“体育迷”与性别有关?
| | 非体育迷 | 体育迷 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | |
附:K2=
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(1) 没有95%的把握认为“体育迷”与性别有关(2) 
解析试题分析:解: (Ⅰ)由频率分布直方图可知,在抽取的100名观众中,“体育迷”共25名,从而完成2×2列联表如下:
2分 非体育迷 体育迷 合计 男 30 15 45 女 45 10 55 合计 75 25 100
将2×2列联表中的数据代入公式计算,得
K2= =
= ≈3.030. 4分
≈3.030. 4分
因为3.030<3.841,所以我们没有95%的把握认为“体育迷”与性别有关. 6分
(Ⅱ)由频率分布直方图可知,“超级体育迷”有5名,从而一切可能结果所组成的基本事件空间为Ω={(a1,a2),(a1,a3),(a2,a3),(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)},其中ai表示男性,i=1,2,3;bj表示女性,j=1,2.
Ω由10个基本事件组成,而且这些基本事件的出现是等可能的. 8分
用A表示“任选2名,至少有1名是女性”这一事件,则
A={(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)},事件A由7个基本事件组成, 10分 因而P(A)= . 11分
. 11分
答:至少有1名女性观众的概率为 12分
12分
考点:本试题考查了古典概型和独立性检验的运用。
点评:对于古典概型的概率计算是一个重要的知识点,需要体会其总的试验空间以及事件发生的基本事件空间,然后利用比值来得到概率的值。而对于独立性检验主要是借助于观测值来分析把握的大小,属于基础题。

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案为了调查胃病是否与生活规律有关,调查某地540名40岁以上的人得结果如下:
| | 患胃病 | 未患胃病 | 合计 |
| 生活不规律 | 60 | 260 | 320 |
| 生活有规律 | 20 | 200 | 220 |
| 合计 | 80 | 460 | 540 |
(本小题满分14分)
某市一家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示:
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
该市煤气收费的方法是:煤气费=基本费十超额费十保险费.
若每月用气量不超过最低额度
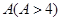 立方米时,只付基本费
立方米时,只付基本费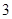 元和每户每月定额保险费
元和每户每月定额保险费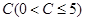 元;若用气量超过
元;若用气量超过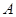 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付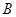 元.
元.(1)根据上面的表格求
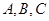 的值;
的值;(2)记用户第四月份用气为
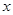 立方米,求他应交的煤气费
立方米,求他应交的煤气费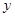 (元).
(元). (本小题满分12分)
某校共有800名学生,高三一次月考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
| 组号 | 第 一 组 | 第 二 组 | 第 三 组 | 第 四 组 | 第 五 组 | 第 六 组 | 第 七 组 | 第 八 组 | 合计 |
| 分组 | 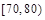 | 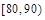 |  | 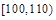 | 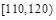 | 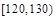 | 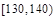 | 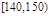 | |
| 频数 | 4 | 6 | 20 | 22 | 18 | 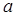 | 10 | 5 | 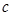 |
| 频率 | 0.04 | 0.06 | 0.20 | 0.22 | 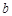 | 0.15 | 0.10 | 0.05 | 1 |
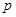 ;
;(Ⅱ)为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生的成绩,并在这6名学生中在随机抽取2名由心理老师张老师负责面谈,求第七组至少有一名学生与张老师面谈的概率;
(Ⅲ)估计该校本次考试的数学平均分。
假设关于某设备的使用年限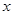 和所支出的维修费用
和所支出的维修费用 (万元)统计数据如下:
(万元)统计数据如下:
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
 对
对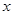 呈线性相关关系.求:
呈线性相关关系.求:(1) 求出线性回归方程
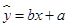 的回归系数;
的回归系数;(2) 估计使用10年时,维修费用是多少。
(本小题12分) 在某化学实验中,测得如下表所示的6组数据,其中x(min)表示化学反应进行的时,y(mg)表示未转化物质的量
| x(min) | l | 2 | 3 | 4 | 5 | 6 |
| y(mg) | 39.8 | 32.2 | 25.4 | 20.3 | 16.2 | 13.3 |
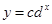 ,试根据测量数据估计c和d的值;
,试根据测量数据估计c和d的值;(2)估计化学反应进行到10 min时未转化物质的量.