题目内容
7. 如图,直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,CA=CB=$\frac{1}{2}$CC1,点D是棱AA1的中点,且C1D⊥BD
如图,直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,CA=CB=$\frac{1}{2}$CC1,点D是棱AA1的中点,且C1D⊥BD(1)求证:CA⊥CB
(2)求直线CD与平面C1BD所成角的正弦值.
分析 (1)证明BC⊥平面ACC1D1,即可证明:CA⊥CB
(2)建立空间直角坐标系,利用向量方法求直线CD与平面C1BD所成角的正弦值.
解答 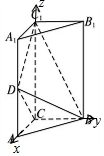 (1)证明:∵四边形ACC1A1为矩形 且D是棱AA1的中点
(1)证明:∵四边形ACC1A1为矩形 且D是棱AA1的中点
∴C1D⊥CD,
又C1D⊥BD且BD∩CD=D,∴C1D⊥平面BCD …(3分)
∵BC?平面BCD,∴C1D⊥BC
又∵BC⊥CC1,且CC1∩C1D=C1,
∴BC⊥平面ACC1D1,
∵AC?平面ACC1D1,
∴BC⊥AC; …(6分)
(2)解:由(1)知:CA,CB,CC1两两相互垂直,
以CA,CB,CC1分别为x,y,z轴的正半轴建立空间直角坐标系,
设CA=CB=1,则C(0,0,0),D(1,0,1),B(0,1,0),C1(0,0,2)…(8分)
设平面C1BD的法向量为$\overrightarrow{m}$=(x,y,z),$\overrightarrow{BD}$=(1,-1,1),$\overrightarrow{{C}_{1}D}$=(1,0,-1)
∴$\left\{\begin{array}{l}{x-y+z=0}\\{x-z=0}\end{array}\right.$取x=1,得$\overrightarrow{m}$=(1,2,1)…(10分)
又$\overrightarrow{CD}$=(1,0,1)
设直线CD与平面C1BD所成角为θ,
则sinθ=$\frac{2}{\sqrt{6}•\sqrt{2}}$=$\frac{\sqrt{3}}{3}$,故直线CD与平面C1BD所成角的正弦值为$\frac{\sqrt{3}}{3}$ …(12分)
点评 本题考查空间直线与平面的位置关系,考查空间的线面角的求法,考查推理能力和空间向量法,及运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 棱台的各侧棱延长后相交于一点 | |
| B. | 如果不在同一平面内的两个相似的直角三角形的对应边互相平行,则连接它们的对应顶点所围成的多面体是三棱台 | |
| C. | 圆台上底圆周上任一点与下底圆周上任一点的连线都是圆台的母线 | |
| D. | 用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台 |
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) | C. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | D. | (-∞,-$\frac{3}{3}$]∪[$\frac{\sqrt{3}}{3}$,+∞) |
| A. | 命题“若x2-4x+3=0,则x=3或x=1”的逆否命题是“若x≠3且x≠1,则x2-4x+3=0≠0” | |
| B. | “x2-x=0”是“x=1”的必要不充分条件 | |
| C. | 若p∨q为真命题,则p,q均为真命题 | |
| D. | 命题p:?x∈R,使得x3+x+1=0,则¬p:?x∈R,使得x3+x+1≠0 |
| A. | 至少有1件次品与至多有1件正品 | B. | 恰有1件次品与恰有2件正品 | ||
| C. | 至少有1件次品与至少有1件正品 | D. | 至少有1件次品与都是正品 |