题目内容
9.设F1是椭圆${x^2}+\frac{y^2}{4}=1$的下焦点,O为坐标原点,点P在椭圆上,则$\overrightarrow{P{F_1}}•\overrightarrow{PO}$的最大值为( )| A. | $4+2\sqrt{3}$ | B. | $4-2\sqrt{3}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}+1$ |
分析 根据椭圆的标准方程求出F1的坐标(0,-$\sqrt{3}$),设P(x,y),求出向量$\overrightarrow{P{F_1}}•\overrightarrow{PO}$的坐标,结合点P满足椭圆的方程,把数量积转化为关于P的横坐标的函数,利用配方法求得最大值.
解答 解:由椭圆的标准方程知F1(0,-$\sqrt{3}$),设P(x,y),
则:$\overrightarrow{P{F_1}}•\overrightarrow{PO}$=(-x,-$\sqrt{3}$-y)•(-x,-y)=${x}^{2}+\sqrt{3}y+{y}^{2}$=1-$\frac{{y}^{2}}{4}$+$\sqrt{3}$y+y2
=$\frac{3}{4}{y}^{2}+\sqrt{3}y+1$=$(\frac{\sqrt{3}}{2}y+1)^{2}$.
∵-2≤y≤2,∴当y=2时,$\overrightarrow{P{F_1}}•\overrightarrow{PO}$取最大值4+2$\sqrt{3}$.
故选:A.
点评 本题主要考查了椭圆的性质,平面向量的数量积,函数的值域,是中档题.

练习册系列答案
相关题目
18.某高校“统计初步”课程的教师为了判断主修统计专业是否与性别有关,随机调查了该选修课的一些学生情况.23名男生中,有10人是统计专业;27名女生中,有20人是统计专业.
(1)根据统计数据填写下面的2×2列联表.
(2)如果判断主修统计专业与性别有关,那么这种判断出错的概率最大不超过多少?
附表:
公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
(1)根据统计数据填写下面的2×2列联表.
| 非统计专业 | 统计专业 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
附表:
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
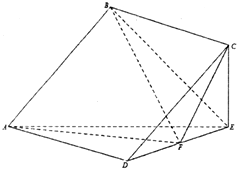 在几何体ABCDE中,四边形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是线段DE的中点.
在几何体ABCDE中,四边形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是线段DE的中点.