题目内容
(本小题满分14分)若函数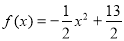 在区间 [a,b]上的最小值为2a,最大值为2b,求[a,b].
在区间 [a,b]上的最小值为2a,最大值为2b,求[a,b].
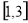 或
或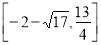
【解析】
试题分析:(1)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动,不论哪种类型,解题的关键是对称轴与区间的关系,当含有参数时,要依据对称轴与区间的关系进行分类讨论;(2)二次函数、二次方程与二次不等式统称“三个”二次,它们常结合在一起,有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法,一般从:①开口方向;②对称轴位置;③判别式;④端点值符合四个方面分析;(3)二次函数的综合问题应用多涉及单调性与最值或二次方程根的分布问题,解决的主要思路是等价转化,多用到数形结合思想与分类讨论思想,
试题解析: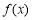 在
在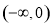 上单调递增,在
上单调递增,在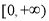 上单调递减. (1分)
上单调递减. (1分)
(1)当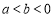 时,假设有
时,假设有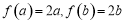 , (2分)
, (2分)
则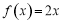 在
在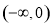 上有两个不等的实根a,b. (4分)
上有两个不等的实根a,b. (4分)
由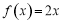 得
得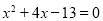 ,
,
因为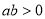 ,所以
,所以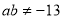 ,故假设不成立. (5分)
,故假设不成立. (5分)
(2)当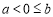 时,假设有
时,假设有 ,即
,即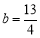 . (6分)
. (6分)
当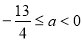 时,
时, ,得
,得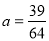 不符合; (7分)
不符合; (7分)
当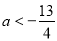 时,
时,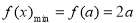 , (8分)
, (8分)
解得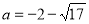 或
或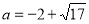 (舍去). (9分)
(舍去). (9分)
(3)当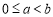 时,假设有
时,假设有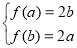 ,即
,即 (11分)
(11分)
解得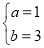 . (13分)
. (13分)
综上所述所求区间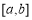 为
为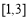 或
或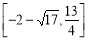 (14分)
(14分)
考点:一元二次函数在闭区间上的最值.

练习册系列答案
相关题目
 ,则目标函数z=2y﹣x的最大值是( )
,则目标函数z=2y﹣x的最大值是( )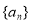 中,
中,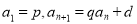 (
( N*,
N*,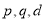 是常数),则
是常数),则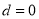 是数列
是数列 中,若
中,若 ,则
,则 .
.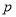 是真命题,
是真命题,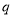 是假命题,则
是假命题,则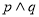 是真命题 B.
是真命题 B.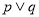 是假命题 C.
是假命题 C.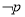 是真命题 D.
是真命题 D.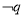 是真命题
是真命题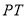 是圆
是圆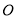 的切线,
的切线,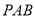 是圆
是圆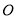 的割线,若
的割线,若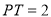 ,
,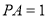 ,
,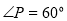 ,则圆
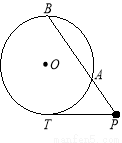
,则圆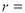 .
.
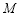 由满足:对任意
由满足:对任意 时,都有
时,都有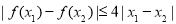 的函数
的函数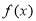 组成.对于两个函数
组成.对于两个函数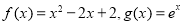 ,以下关系成立的是
,以下关系成立的是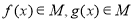 B.
B.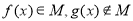
 D.
D.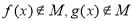
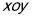 中,设
中,设 是由不等式组
是由不等式组 表示的区域,
表示的区域, 是到原点的距离不大于
是到原点的距离不大于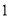 的点构成的区域,向
的点构成的区域,向 中随机投一点,则所投点落在
中随机投一点,则所投点落在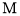 中的概率是 .
中的概率是 . ,
,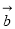 ,两组向量
,两组向量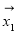 、
、 、
、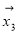 、
、 、
、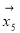 和
和 、
、 、
、 、
、 、
、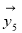 均由2个
均由2个 +
+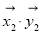 +
+ +
+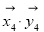 +
+ ,Smin表示S所有可能取值中的最小值.则下列所给5个命题中,所有正确的命题的序号是 .
,Smin表示S所有可能取值中的最小值.则下列所给5个命题中,所有正确的命题的序号是 .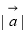 无关;
无关; 无关;④若
无关;④若 ,则Smin>0;
,则Smin>0; ,Smin=
,Smin=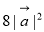 ,则
,则 .
.