题目内容
若命题“?x∈R,使得x2+(1-a)x<0”是假命题,则实数a的取值范围是 .
考点:特称命题
专题:简易逻辑
分析:根据一元二次不等式的解法,我们先求出“?x∈R,使得x2+(1-a)x<0”是真命题时,实数a的取值范围,再利用补集的求法,即可得到命题“?x∈R,使得x2+(1-a)x<0”是假命题,实数a的取值范围.
解答:
解:若命题“?x∈R,使得x2+(1-a)x<0”成立
则对应方程x2+(1-a)x<0一定有两个不等的根
即△=(1-a)2>0
即a≠1,
则命题“?x∈R,使得x2+(a+2)x+1<0”是假命题时
数a的取值范围是{1},
故答案为:{1}.
则对应方程x2+(1-a)x<0一定有两个不等的根
即△=(1-a)2>0
即a≠1,
则命题“?x∈R,使得x2+(a+2)x+1<0”是假命题时
数a的取值范围是{1},
故答案为:{1}.
点评:本题考查的知识点是命题的真假判断与应用,其中根据二次不等式的解法求出“?x∈R,使得x2+(a+2)x+1<0”是真命题时,实数a的取值范围,是解答本题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

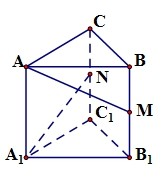 13、如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,若M,N分别是BB1,CC1的中点,则异面直线AM与A1N所成的角的大小为
13、如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,若M,N分别是BB1,CC1的中点,则异面直线AM与A1N所成的角的大小为