题目内容
15.下列函数中,既是偶函数又在区间(0,+∞)上是单调增函数的是( )| A. | $y=\frac{1}{x}$ | B. | y=|x|-1 | C. | y=lgx | D. | $y={({\frac{1}{2}})^{|x|}}$ |
分析 利用基本函数的奇偶性、单调性逐项判断即可.
解答 解:对于A,y=$\frac{1}{x}$为定义域上的奇函数,不满足题意;
对于B,y=|x|-1,是定义域R上的偶函数,且在(0,+∞)上是单调增函数,满足题意;
对于C,y=lgx是非奇非偶的函数,不满足题意;
对于D,y=${(\frac{1}{2})}^{|x|}$是定义域上的偶函数,但在(0,+∞)上单调递减,不满足题意.
故选:B.
点评 本题考查了函数的奇偶性与单调性的判断问题,熟记基本函数的有关性质是解题的关键,是基础题目.

练习册系列答案
相关题目
5.已知i是虚数单位,复数z=1+2i,则$i\overline z$=( )
| A. | 2-i | B. | 2+i | C. | -2-i | D. | -2+i |
6.函数y=x2cosx的部分图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
20.已知x,y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x+y-2≥0\\ x≤2\end{array}\right.$,则目标函数z=2x-y的最大值为( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | 4 | D. | 5 |
7.已知集合A={0,1,2},B={m,3,4},若A∩B={2},则实数m=( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
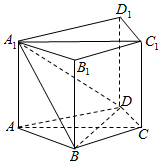 如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.
如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.