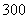题目内容
已知抛物线 (
( )的准线与
)的准线与 轴交于点
轴交于点
 .
.
(1)求抛物线的方程,并写出焦点坐标;
(2)是否存在过焦点的直线 (直线与抛物线交于点
(直线与抛物线交于点 ,
, ),使得三角形
),使得三角形 的面积
的面积
 ?若存在,请求出直线
?若存在,请求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(1)由已知得: ,从而抛物线方程为
,从而抛物线方程为 ,焦点坐标为
,焦点坐标为 .
.
(2)解法一:由题意,设
 ,并与
,并与 联立, 得到方程:
联立, 得到方程: ,
,
设 ,
, ,则
,则 ,
, . 7分
. 7分

∵ ,∴
,∴

 , 9分
, 9分
又 ,∴
,∴ 解得
解得 , 11分
, 11分
故直线 的方程为:
的方程为: .即
.即 或
或 . 12分
. 12分
解法二:当 轴时,
轴时, ,
, ,不合题
,不合题
故设
 (
( ),并与
),并与 联立,到方程:
联立,到方程: ,
,
设 ,
, ,则
,则 ,
, .
. 
 ,
,
点 到直线
到直线 的距离为
的距离为 , 9分
, 9分
∴

 , 10分
, 10分
解得 ,故直线
,故直线 的方程为:
的方程为: .即
.即 或
或 . 12分
. 12分
考点:1.抛物线的性质.2.直线与抛物线的关系.3.弦长公式,点到直线的距离.4.运算能力.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 的内角A、B、C所对的边长分别为
的内角A、B、C所对的边长分别为 ,且
,且 ,
, 。
。 时,求
时,求 的值.
的值. 的值.
的值. 的图象是曲线
的图象是曲线 ,其中点
,其中点 ,则
,则

 分别是双曲线
分别是双曲线 的左、右焦点,以坐标原点
的左、右焦点,以坐标原点 为
为 为半径的圆与双曲线在第一象限的交点为
为半径的圆与双曲线在第一象限的交点为 ,则当
,则当 的面积等于
的面积等于 时,
时, B.
B. C.
C. D.2
D.2  中,曲线
中,曲线 的焦点
的焦点 ,点
,点 在曲线
在曲线 上,
上, ,则
,则 .
. 之间的大小关系是( )
之间的大小关系是( ) (B)
(B)  (C)
(C)  (D)
(D) 
 在
在 是单调递减的,则
是单调递减的,则 的范围是( )
的范围是( ) (B)
(B) (C)
(C) (D)
(D)
 与
与 呈相关关系,且由观测数据得到的样本数据散点图如图所示,则由该观测数据算得的回归方程可能是( )
呈相关关系,且由观测数据得到的样本数据散点图如图所示,则由该观测数据算得的回归方程可能是( ) .
.
 .
.
 .
.
 .
.

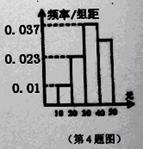
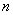 个同学进行调查,结果显示这些同学的支出都在
个同学进行调查,结果显示这些同学的支出都在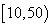 (单位:元),其中支出在
(单位:元),其中支出在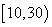 (单位:元)的同学有
(单位:元)的同学有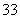 人,其频率分布直方图如下图所示,则支出在
人,其频率分布直方图如下图所示,则支出在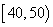 (单位:元)的同学人数是( )
(单位:元)的同学人数是( )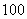 B.
B.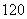 C.
C.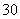 D.
D.