题目内容
右表是一个由正数组成的数表,数表中各行依次成等差数列,各列依次成等比数列,且公比都相等,已知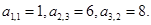

(1)求数列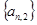 的通项公式;
的通项公式;
(2)设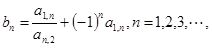 求数列
求数列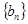 的前
的前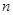 项和
项和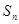 。
。
(1)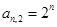 ;(2)
;(2)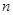 为偶数时,
为偶数时,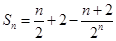 ,
,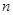 为奇数时,
为奇数时,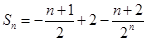 .
.
解析试题分析:(1)通过读表得到表达式,利用等差等比数列的通项公式将表达式展开,求出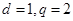 ,得到数列
,得到数列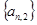 的通项公式;(2)将第一问的结论代入,先用分组求和法,将式子分成两组,再用错位相减法求第一部分,第二部分用并项法求和.
的通项公式;(2)将第一问的结论代入,先用分组求和法,将式子分成两组,再用错位相减法求第一部分,第二部分用并项法求和.
试题解析:(1)设第一行依次组成的等差数列的公差是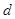 ,等比数列的公比是
,等比数列的公比是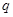
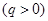 ,
,
则 , 2分
, 2分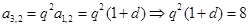 , 4分
, 4分
解得: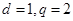 ,所以:
,所以: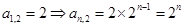 ; 6分
; 6分
(2)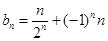 ,
,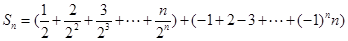 , 8分
, 8分
记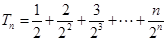 ,则
,则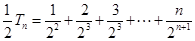 ,
,
两式相减得: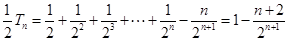 ,所以
,所以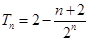 , 10分
, 10分
所以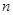 为偶数时,
为偶数时,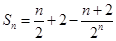 ,
,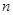 为奇数时,
为奇数时,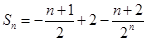 。 12分
。 12分
考点:1.等差等比数列的通项公式;2.分组求和法;3.错位相减法.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
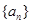 满足:
满足: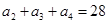 ,且
,且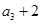 是
是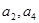 的等差中项.
的等差中项.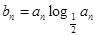 ,
,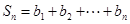 ,求使
,求使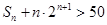 成立的正整数
成立的正整数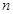 的最小值.
的最小值.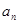 }中,
}中,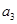 =3,前7项和
=3,前7项和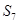 =28。
=28。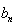 }为等比数列,且
}为等比数列,且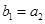 ,
,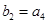 求数列
求数列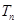
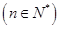 .
.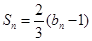 且
且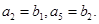
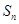 是数列
是数列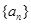 的前
的前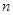 项和,
项和,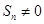 ,
,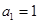 ,
,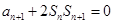 .
.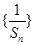 是等差数列,并
是等差数列,并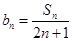 ,求数列
,求数列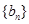 的前
的前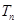 .
. (
(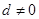 )的等差数列
)的等差数列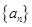 与公比为
与公比为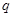 (
(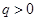 )的等比数列
)的等比数列 有如下关系:
有如下关系: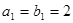 ,
,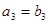 ,
,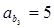 .
.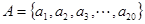 ,
,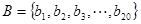 ,
,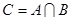 ,求集合
,求集合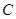 中的各元素之和。
中的各元素之和。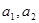 是方程x2-14x+45=0的两根,求数列
是方程x2-14x+45=0的两根,求数列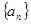 通项公式(2)设
通项公式(2)设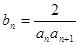 ,数列{bn}的前n项和为Sn,证明
,数列{bn}的前n项和为Sn,证明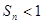 .
.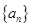 满足
满足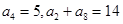 ,数列
,数列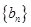 满足
满足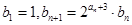 .
.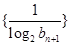 的前
的前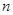 项和;
项和;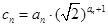 ,求数列
,求数列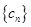 的前
的前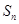 .
.