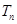题目内容
已知等差数列{an}的前n项和为 Sn
(I)若a1=1,S10= 100,求{an}的通项公式;
(II)若Sn=n2-6n,解关于n的不等式Sn+an>2n
(I)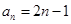 ; (II)
; (II)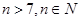 .
.
解析试题分析:(I)要求等差数列的通项公式,由已知条件只需再找到d即可,由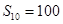 结合等差数列的前n项和公式很快即可解决该问题; (II)先由
结合等差数列的前n项和公式很快即可解决该问题; (II)先由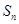 ,结合
,结合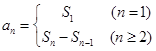 求出该等差数列的通项
求出该等差数列的通项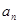 ,代入条件即可将该问题转化为一元二次不等式的问题.
,代入条件即可将该问题转化为一元二次不等式的问题.
试题解析:
(I)设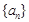 的公差为
的公差为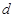
因为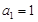 ,
, 2分
2分
所以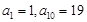 4分
4分
所以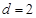
所以 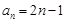 ; 6分
; 6分
(II)因为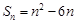
当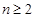 时,
时,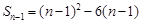
所以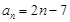 ,
,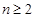 9分
9分
又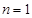 时,
时,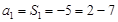
所以 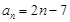 10分
10分
所以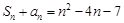
所以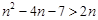 ,即
,即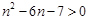
所以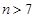 或
或 ,
,
所以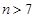 ,
,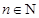 . 13分
. 13分
考点:等差数列的通项公式及前n项和公式.

练习册系列答案
相关题目
 是等差数列,且
是等差数列,且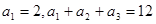
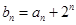 ,求数列
,求数列 前n项和
前n项和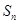 .
. 是首项是2,公比为q的等比数列,其中
是首项是2,公比为q的等比数列,其中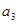 是
是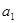 与
与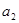 的等差中项.
的等差中项. 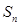
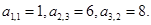

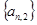 的通项公式;
的通项公式;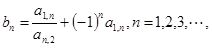 求数列
求数列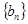 的前
的前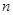 项和
项和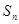 。
。 的首项
的首项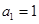 ,公差
,公差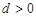 .且
.且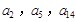 分别是等比数列
分别是等比数列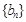 的
的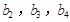 .
. 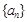 与
与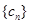 对任意自然数
对任意自然数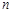 均有
均有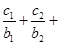
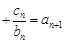 成立,求
成立,求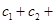
 的值.
的值.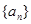 中,
中, ,
,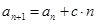 (
(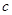 是不为零的常数,
是不为零的常数,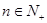 ),且
),且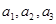 成等比数列.
成等比数列. 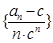 的前n项之和为
的前n项之和为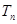 ,求证
,求证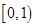 。
。 的前
的前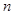 项和为
项和为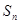 ,已知
,已知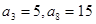 .
. ;
;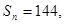 求
求 中,
中, 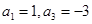
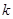 项和
项和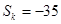 ,求
,求 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列, 为
为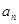 及
及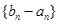 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列 的通项公式及其前n项和
的通项公式及其前n项和