题目内容
函数f(x)=x×|x-1|-3x+1的递减区间是 .
考点:函数的单调性及单调区间
专题:计算题,函数的性质及应用
分析:通过对x-1≤0与x-1≥0的讨论,去掉绝对值符号,转化为二次函数,利用该区间上二次函数的单调性即可求得答案.
解答:
解:①当x-1≤0即x≤1时:
f(x)=x-x2-3x+1=-x2-4x+1,对称轴为:x=-2,开口向下,
∴此时f(x)=x|x-1|-3x+1的单调递减区间为[-2,1];
②当x-1≥0即x≥1时:
∴f(x)=x2-x-3x+1=x2-4x+1,函数的对称轴为x=2,开口向上,
∴此时f(x)=x|x-1|-3x+1的单调递减区间为[1,2]
综上所述,f(x)=x|x-1|-3x+1的单调递减区间为[-2,1],[1,2].又函数在x=1时函数连续,
属于函数的递减区间:[-2,2].
故答案为:[-2,2].
f(x)=x-x2-3x+1=-x2-4x+1,对称轴为:x=-2,开口向下,
∴此时f(x)=x|x-1|-3x+1的单调递减区间为[-2,1];
②当x-1≥0即x≥1时:
∴f(x)=x2-x-3x+1=x2-4x+1,函数的对称轴为x=2,开口向上,
∴此时f(x)=x|x-1|-3x+1的单调递减区间为[1,2]
综上所述,f(x)=x|x-1|-3x+1的单调递减区间为[-2,1],[1,2].又函数在x=1时函数连续,
属于函数的递减区间:[-2,2].
故答案为:[-2,2].
点评:本题考查函数单调性的判断与证明,通过讨论去掉绝对值符号是关键,考查分类讨论思想与运算能力,属于中档题.

练习册系列答案
相关题目
若函数f(x)=xcosx在(0,+∞)内的全部极值点按从小到大的顺序排列为a1,a2,…,an,…,则对任意正整数n必有( )
A、π<an+1-an<
| ||
B、
| ||
C、0<an+1-an<
| ||
D、-
|
已知角α终边上一点P(
,1),则2sin2α-3tanα=( )
| 3 |
A、-1-3
| ||
B、1-3
| ||
C、-2
| ||
| D、0 |
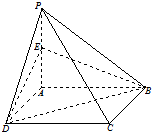 如图:在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E为PA中点.
如图:在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,E为PA中点.