题目内容
15.已知曲线C的极坐标方程是ρ=4sinθ,设直线l的参数方程$\left\{\begin{array}{l}x=-\frac{3}{5}t+2\\ y=\frac{4}{5}t\end{array}\right.(t$为参数).(1)将曲线C的极坐标方程转化为直角坐标方程;
(2)设直线l与曲线C的交点是M,N,求|MN|.
分析 (1)直接利用极坐标与直角坐标方程的互化求解即可.
(2)求出直线l的直角坐标方程,求出圆的圆心与半径,利用垂径定理求解即可.
解答 解:(1)ρ2=4ρsinθ,∴x2+y2=4y即x2+y2-4y=0…(5分)
(2)直线l的直角坐标方程为4x+3y-8=0…(7分)
曲线C为以P(0,2)为圆心,2为半径的圆,P到直线l的距离$d=\frac{2}{5}$,
$|MN|=2\sqrt{4-{{(\frac{2}{5})}^2}}=\frac{{8\sqrt{6}}}{5}$…(10分)
点评 本题考查极坐标与直线的参数方程的应用,垂径定理的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知x与y之间的一组数据:
则y与x的线性回归方程为$\hat y=bx+a$必过点(2.5,2).
| x | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 |
7.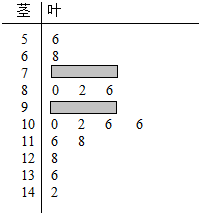 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
(1)求表中a,b的值
(2)求分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格);
(3)从成绩在[100,130)范围内的学生中随机选4人,求其中成绩在[100,110)内的人数最多2人的概率.
 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:| 分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
| 频数 | b | |||||
| 频率 | a | 0.25 |
(2)求分数在[90,100)范围内的学生人数,并估计这次考试全校学生数学成绩的及格率(分数在[90,150)内为及格);
(3)从成绩在[100,130)范围内的学生中随机选4人,求其中成绩在[100,110)内的人数最多2人的概率.
4.下列式子中表示正确的是( )
| A. | 2+cosx=4 | B. | $\sqrt{10}$>π | C. | sinx•cosx=sin2x | D. | sin75°>cos14° |
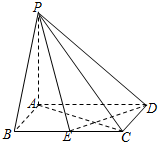 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,点E为BC的中点.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,点E为BC的中点.