题目内容
12.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{-{x}^{2}+4x-3},1≤x≤3}\\{{2}^{x}-8,x>3}\end{array}\right.$,若F(x)=f(x)-kx在其定义域内有3个零点,则实数k∈(0,$\frac{\sqrt{3}}{3}$).分析 问题转化为f(x)和y=kx有3个交点,画出函数f(x)和y=kx的图象,求出临界值,从而求出k的范围即可.
解答 解:若F(x)=f(x)-kx在其定义域内有3个零点,
即f(x)和y=kx有3个交点,
画出函数f(x)和y=kx的图象,如图示: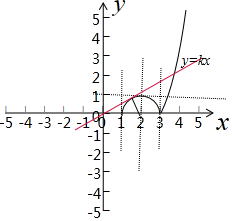 ,
,
点(2,0)到直线y=kx的距离d=$\frac{|2k|}{\sqrt{1{+k}^{2}}}$=1,
解得:k=$\frac{\sqrt{3}}{3}$,
故:0<k<$\frac{\sqrt{3}}{3}$;
故答案为:(0,$\frac{\sqrt{3}}{3}$).
点评 本题考查了函数的零点问题,考查数形结合思想以及点到直线的距离,是一道中档题.

练习册系列答案
相关题目
3.某班班会准备从含甲、乙的6名学生中选取4人发言,要求甲、乙两人至少有一人参加,那么不同的发言顺序有( )
| A. | 336种 | B. | 320种 | C. | 192种 | D. | 144种 |
20.已知空间两条直线m,n两个平面α,β,给出下面四个命题:
①m∥n,m⊥α⇒n⊥α;
②α∥β,m?α,n?β⇒n⊥α;
③m∥n;m∥α⇒n∥α
④α∥β,m∥n,m⊥α⇒n⊥β.
其中正确的序号是( )
①m∥n,m⊥α⇒n⊥α;
②α∥β,m?α,n?β⇒n⊥α;
③m∥n;m∥α⇒n∥α
④α∥β,m∥n,m⊥α⇒n⊥β.
其中正确的序号是( )
| A. | ①④ | B. | ②③ | C. | ①②④ | D. | ①③④ |
4.在下列各区间中,存在着函数f(x)=x3+4x-3的零点的区间是( )
| A. | [-1,0] | B. | [0,1] | C. | [1,2] | D. | [2,3] |