题目内容
已知函数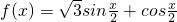
(Ⅰ) 求f(x)的周期、对称中心、对称轴和单调递增区间;
(Ⅱ) 当x∈[0,π]时,求f(x)的值域.
解:(I)f(x)=2( sin
sin +
+ cos
cos )=2sin(
)=2sin( +
+ )
)
∴T=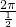 =4π
=4π
令 +
+ =kπ,得x=2kπ-
=kπ,得x=2kπ-
∴f(x)图象的对称中心为(2kπ- ,0)
,0)
令 +
+ =kπ+
=kπ+ ,得x=2kπ+
,得x=2kπ+
∴f(x)的对称轴为x=2kπ+
令2kπ- ≤
≤ +
+ ≤2kπ+
≤2kπ+
得4kπ- ≤x≤4kπ+
≤x≤4kπ+
∴f(x)的递增区间为[4kπ- ,4kπ+
,4kπ+ ]
]
(II)由x∈[0,π],得 ,
,
∴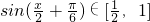
∴函数f(x)值域为[1,2]
分析:(I)先将函数转化成f(x)=2sin( +
+ ),然后根据T=
),然后根据T=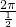 =4π,对称中心
=4π,对称中心 +
+ =kπ,对称轴
=kπ,对称轴 +
+ =kπ+
=kπ+ ,单调递增区间2kπ-
,单调递增区间2kπ- ≤
≤ +
+ ≤2kπ+
≤2kπ+ ,再将x求出即可.
,再将x求出即可.
(II)先求出 ,然后根据正弦函数的特点求出值域.
,然后根据正弦函数的特点求出值域.
点评:本题考查了正弦函数的定义域、值域、对称性、单调性、周期性等知识,熟练掌握知识可以提高做题效率,属于中档题.
 sin
sin +
+ cos
cos )=2sin(
)=2sin( +
+ )
)∴T=
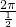 =4π
=4π令
 +
+ =kπ,得x=2kπ-
=kπ,得x=2kπ-
∴f(x)图象的对称中心为(2kπ-
 ,0)
,0)令
 +
+ =kπ+
=kπ+ ,得x=2kπ+
,得x=2kπ+
∴f(x)的对称轴为x=2kπ+

令2kπ-
 ≤
≤ +
+ ≤2kπ+
≤2kπ+
得4kπ-
 ≤x≤4kπ+
≤x≤4kπ+
∴f(x)的递增区间为[4kπ-
 ,4kπ+
,4kπ+ ]
](II)由x∈[0,π],得
 ,
,∴
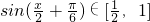
∴函数f(x)值域为[1,2]
分析:(I)先将函数转化成f(x)=2sin(
 +
+ ),然后根据T=
),然后根据T=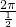 =4π,对称中心
=4π,对称中心 +
+ =kπ,对称轴
=kπ,对称轴 +
+ =kπ+
=kπ+ ,单调递增区间2kπ-
,单调递增区间2kπ- ≤
≤ +
+ ≤2kπ+
≤2kπ+ ,再将x求出即可.
,再将x求出即可.(II)先求出
 ,然后根据正弦函数的特点求出值域.
,然后根据正弦函数的特点求出值域.点评:本题考查了正弦函数的定义域、值域、对称性、单调性、周期性等知识,熟练掌握知识可以提高做题效率,属于中档题.

练习册系列答案
相关题目
 .
.
 .
. 上的最大值和最小值.
上的最大值和最小值. .
. ,求f(α).
,求f(α). .
. 上的最大值和最小值.
上的最大值和最小值.