题目内容
已知一个几何体的三视图如图所示,则这个几何体的体积为 .


考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知的三视图可得:该几何体是一个以俯视图为底面的三棱锥,求出底面面积和高,代入棱锥体积公式,可得答案.
解答:
解:由由已知的三视图可得:该几何体是一个以俯视图为底面的三棱锥,
其底面面积S=
×1×1=
,
高h=2,
故这个几何体的体积V=Sh=
×
×2=
,
故答案为:
其底面面积S=
| 1 |
| 2 |
| 1 |
| 2 |
高h=2,
故这个几何体的体积V=Sh=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查的知识点是由三视图求体积和表面积,其中根据已知的三视图分析出几何体的形状,是解答的关键.

练习册系列答案
相关题目
直线l经过点M(1,2),且被圆:x2+y2=25所截得的弦长最短,则直线l的方程为( )
| A、2x-y=0 |
| B、2x+y-4=0 |
| C、x+2y+5=0 |
| D、x+2y-5=0 |
甲乙二人同时从A地赶往B地,甲先骑自行车到中点后改为跑步,而乙则是先跑步,到中点后改为骑自行车,最后二人同时到达B地,甲乙两人骑自行车速度都大于各自跑步速度,又知甲骑自行车比乙骑自行车的速度快.若某人离开A地的距离S与所用时间t的函数用图象表示如下,则在下列给出的四个函数中
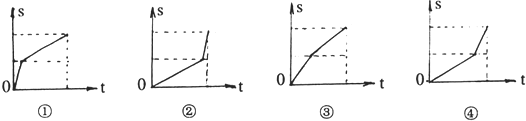
甲乙二人的图象只可能( )

甲乙二人的图象只可能( )
| A、甲是图①,乙是图② |
| B、甲是图①,乙是图④ |
| C、甲是图③,乙是图② |
| D、甲是图③,乙是图④ |
计算sin
=( )
| 7π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列关于三个数log0.53,lnπ,(a2+3)0(a∈R)的大小关系,正确的是( )
| A、log0.53<(a2+3)0<lnπ |
| B、log0.53<lnπ<(a2+3)0 |
| C、(a2+3)0<log0.53<lnπ |
| D、lnπ<(a2+3)0<log0.53 |
设y1=20.3,y2=(
)0.4,y3=log3
则( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、y3>y1>y2 |
| B、y2>y1>y3 |
| C、y1>y3>y2 |
| D、y1>y2>y3 |