题目内容
如图,在四棱锥O—ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点。
(1)求证:直线BD⊥平面OAC;
(2)求直线MD与平面OAC所成角的大小;
(3)求点A到平面OBD的距离。
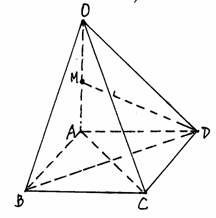
解:方法一:以A为原点,AB,AD,AO分别x轴,y轴,z轴建立空间直角坐标系,A-xyz。
(1)∵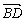 =(-1,1,0),
=(-1,1,0),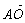 =(0,0,2),
=(0,0,2),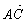 =(1,1,0)
=(1,1,0)
∴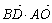 =0,
=0,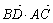 =-1+1=0
=-1+1=0
∴BD⊥AD,BD⊥AC,又AO∩AC=A
故BD⊥平面OAC
(2)取平面OAC的法向量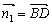 =(-1,1,0),又
=(-1,1,0),又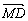 =(0,1,-1)
=(0,1,-1)
则: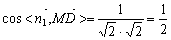
∴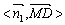 =60°
=60°
故:MD与平面OAC所成角为30°
(3)设平面OBD的法向量为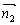 =(x,y,z),则
=(x,y,z),则
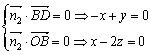
取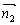 =(2,2,1)
=(2,2,1)
则点A到平面OBD的距离为d=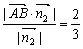
方法二:(1)由OA⊥底面ABCD,OA⊥BD。
∵底面ABCD是边长为1的正方形
∴BD⊥AC ∴BD⊥平面OAC
(2)设AC与BD交于点E,连结EM,则∠DME是直线MD与平面OAC折成的角
∵MD=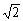 ,DE=
,DE=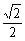
∴直线MD与平面OAC折成的角为30°
(3)作AH⊥OE于点H。
∵BD⊥平面OAC
∴BO⊥AH
线段AH的长就是点A到平面OBD的距离。
∴AH=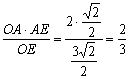
∴点A到平面OBD的距离为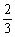

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
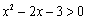 ”是 “
”是 “ ”的必要不充分条件,则
”的必要不充分条件,则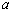 的最大值为 .
的最大值为 .
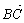 >0;条件乙:点C的坐标是方程
>0;条件乙:点C的坐标是方程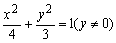 的解,则甲是乙的
的解,则甲是乙的
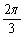 )
)
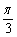 )
)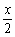 -
-