题目内容
【题目】设椭圆![]()
![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,椭圆的上顶点为点
,椭圆的上顶点为点![]() ,点
,点![]() 为椭圆
为椭圆![]() 上一点,且
上一点,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,求线段
两点,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
![]() 利用向量的坐标表示及运算表示出点
利用向量的坐标表示及运算表示出点![]() 坐标,代入椭圆
坐标,代入椭圆![]() 的方程即可求解;
的方程即可求解;
![]() 由
由![]() 知
知![]() ,结合
,结合![]() 求出椭圆
求出椭圆![]() 的方程,分两种情况线段
的方程,分两种情况线段![]() 在
在![]() 轴上和线段
轴上和线段![]() 不在
不在![]() 轴上求解点
轴上求解点![]() ,当线段
,当线段![]() 不在
不在![]() 轴上, 设直线
轴上, 设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,代入椭圆方程,利用韦达定理和中点坐标公式,消去参数
,代入椭圆方程,利用韦达定理和中点坐标公式,消去参数![]() 即可.
即可.
(1) 设![]() (
(![]() ),
),![]()
![]() ,
,![]() ,
,
所以![]() ,
,![]() 得
得
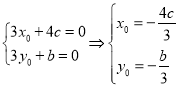 ,即
,即![]() ,
,
又∵![]() (
(![]() )在椭圆
)在椭圆![]()
![]() 上,
上,
∴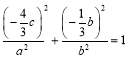 ,得
,得![]() ,即椭圆
,即椭圆![]() 的离心率为
的离心率为![]() .
.
(2) 由(1)知,![]() .又∵
.又∵![]() ,
,![]() ,
,
解得![]() ,
,![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
当线段![]() 在
在![]() 轴上时,线段
轴上时,线段![]() 的中点
的中点![]() 为坐标原点(0,0).
为坐标原点(0,0).
当线段![]() 不在
不在![]() 轴上时,设直线
轴上时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
将直线![]() 的方程为
的方程为![]() 代入椭圆方程
代入椭圆方程![]() 中,得
中,得![]() .
.
∵点![]() 在椭圆内部,∴
在椭圆内部,∴![]() ,
,![]() ,则
,则![]() ,
,
∴点![]() 的坐标满足
的坐标满足![]() ,
,![]() ,消去
,消去![]() 得,
得,![]() (
(![]() ).
).
综上所述,点![]() 的轨迹方程为
的轨迹方程为![]() .
.

练习册系列答案
相关题目
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
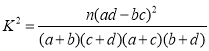 (其中
(其中![]() ).
).