题目内容
【题目】已知函数![]() .
.
(Ⅰ)若直线![]() 在点
在点![]() 处切线方程为
处切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)若函数![]() 有3个零点,求实数
有3个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)求出导函数![]() ,根据题意利用导数的几何意义可得
,根据题意利用导数的几何意义可得![]() ,求解即可.
,求解即可.
(Ⅱ)将函数转化为![]() ,从而可得方程
,从而可得方程![]() 有2个不为1的不等实数根,然后分离参数后则有函数
有2个不为1的不等实数根,然后分离参数后则有函数![]() 与
与![]() 图象有两个交点,利用导数画出
图象有两个交点,利用导数画出![]() 的简图,利用数形结合即可求解.
的简图,利用数形结合即可求解.
(Ⅰ)因为![]() ,
,
得![]() ,
,
所以![]() .
.
因为曲线在点![]() 处的切线方程为
处的切线方程为![]() ,
,
所以![]() ,即
,即![]() .
.
(Ⅱ)![]() ,
,
所以![]() 有一个零点
有一个零点![]() .
.
要使得![]() 有3个零点,即方程
有3个零点,即方程![]() 有2个不为1的不等实数根,
有2个不为1的不等实数根,
又方程![]() ,令
,令![]() ,
,
即函数![]() 与
与![]() 图象有两个交点,
图象有两个交点,
令![]() ,得
,得![]() .
.
![]() 的单调性如表:
的单调性如表:
|
|
| 1 |
|
| - | - | 0 | + |
|
|
| 极小值 |
|
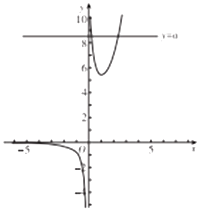
当![]() 时,
时,![]() ,又
,又![]() ,
,
可作出![]() 的大致图象,由图象得
的大致图象,由图象得![]()
所以,要使得![]() 有3个零点,
有3个零点,
则实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】某省开展“精准脱贫,携手同行”的主题活动,某贫困县统计了100名基层干部走访贫困户的数量,并将走访数量分成5组,统计结果见下表.
走访数量区间 | 频数 | 频率 |
| b | |
| 10 | |
| 38 | |
| a | 0.27 |
| 9 | |
总计 | 100 | 1.00 |
(1)求a与b的值;
(2)根据表中数据,估计这100名基层干部走访数量的中位数(精确到个位);
(3)如果把走访贫困户不少于35户视为“工作出色”,按照分层抽样,从“工作出色”的基层干部中抽取4人,再从这4人中随机抽取2人,求其中有1人走访贫困户不少于45户的概率.