题目内容
7.已知定义域为R的函数f(x)=$\frac{{-{2^x}+n}}{{{2^{x+1}}+m}}$是奇函数.①求m、n的值;
②若对任意的t∈(1,2),不等式f(t2-2t)+f(2t2-k)<0恒成立,求实数k的取值范围.
分析 (1)利用函数奇偶性的性质建立方程关系即可求m、n的值;
(2)根据函数解析式求出函数的单调性,利用参数分离法进行求解即可.
解答 解:(1)因为f(x)是奇函数,所以f(0)=0
即$\frac{-1+n}{2+m}$=0,∴n=1,
∴f(x)=$\frac{-{2}^{x}+1}{{2}^{x+1}+m}$,
∵f(1)=-f(-1),
∴$\frac{-2+1}{4+m}$=-$\frac{-\frac{1}{2}+1}{1+m}$,
∴m=2…(5分)
(2)由①知$f(x)=\frac{{-{2^x}+1}}{{{2^{x+1}}+2}}=-\frac{1}{2}+\frac{1}{{{2^x}+1}}$
由上式知f(x)在(-∞,+∞)上为减函数
∵f(x)是奇函数
∴f(t2-2t)+f(2t2-k)<0等价于f(t2-2t)<-f(2t2-k)=f(-2t2+k)
又∵f(x)在(-∞,+∞)上为减函数
由上式推得t2-2t>-2t2+k,即对一切t∈(1,2)有3t2-2t>k恒成立
令u(t)=3t2-2t,t∈(1,2)
则函数u(t)=3t2-2t在(1,2)上单调递增
∴u(t)>1
∴实数k的取值范围为{k|k≤1}…(12分)
点评 本题主要考查函数奇偶性的应用,以及不等式恒成立,利用函数奇偶性的定义建立方程关系是解决本题的关键.

练习册系列答案
相关题目
15.已知a<0,函数f(x)=ax2+bx+c,若x0满足2ax+b=0,则下列必为真命题的是( )
| A. | ?x∈R,f(x)>f(x0) | B. | ?x∈R,f(x-1)≥f(x0) | C. | ?x∈R,f(x)≤f(x0) | D. | ?x∈R,f(x+1)≥f(x0) |
19.下列函数中,定义域是R且为增函数的是( )
| A. | y=(x-1)2 | B. | y=x3 | C. | y=$\frac{1}{x}$ | D. | y=|x| |
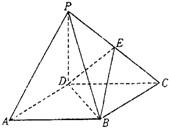 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.