题目内容
17.设函数f(x)是定义在R上的偶函数,f′(x)为其导函数,当x>0时,f(x)+x•f′(x)>0,且f(1)=0,则不等式x•f(x)>0的解集为(-1,0)∪(1,+∞).分析 由题意可得函数g(x)=xf(x)是R上的奇函数,画出函数g(x)=xf(x)的单调性的示意图,数形结合求得不等式x•f(x)>0的解集.
解答 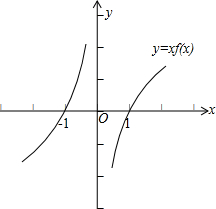 解:∵(x•f(x))′=f(x)+x•f′(x)>0,
解:∵(x•f(x))′=f(x)+x•f′(x)>0,
故函数g(x)=xf(x)在(0,+∞)上单调递增.
再根据函数f(x)是定义在R上的偶函数,
可得函数g(x)=xf(x)是R上的奇函数,
故函数g(x)=xf(x)是R上的奇函数,
故函数g(x)=xf(x)在(-∞,0)上单调递增.
∵f(1)=0,∴f(-1)=0,
故函数y=xf(x)的单调性的示意图,如图所示:
由不等式x•f(x)>0,
可得 x与f(x)同时为正数或同时为负数,∴x>1,或-1<x<0,
故不等式x•f(x)>0的解集为:(-1,0)∪(1,+∞),
故答案为:(-1,0)∪(1,+∞).
点评 本题主要考查函数的奇偶性的性质,函数的导数与单调性的关系,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
8.数列{an}满足:an+1=3an+2,且a1=1,则其通项公式an=( )
| A. | 3n-1 | B. | 2×3n-1 | C. | 2×3n-1-1 | D. | 3n-1-1 |
5.已知α为锐角,且cos(α+$\frac{π}{12}}$)=$\frac{3}{5}$,则sin2α的值为( )
| A. | $\frac{{24-7\sqrt{3}}}{50}$ | B. | $\frac{{24+7\sqrt{3}}}{50}$ | C. | $\frac{{24\sqrt{3}-7}}{50}$ | D. | $\frac{{24\sqrt{3}+7}}{50}$ |
12.集合A={0,1,2,3,4},B={x|(x+2)(x-1)≤0},则A∩B=( )
| A. | {0,1,2,3,4} | B. | {0,1,2,3} | C. | {0,1,2} | D. | {0,1} |
6.一个三角形的三边成等比数列,则公比q的范围是( )
| A. | q>$\frac{\sqrt{5}+1}{2}$ | B. | q<$\frac{\sqrt{5}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$<q<$\frac{\sqrt{5}+1}{2}$ | D. | q<$\frac{\sqrt{5}-1}{2}$或q>$\frac{\sqrt{5}+1}{2}$ |
7.下列四个数中数值最大的是( )
| A. | 1111(2) | B. | 16 | C. | 23(7) | D. | 30(6) |