题目内容
11.平面直角坐标系xOy中,抛物线C的顶点在坐标原点,焦点为双曲线${x^2}-\frac{y^2}{3}=1$的右顶点.(1)求抛物线C的方程;
(2)经过已知双曲线的左焦点作抛物线C的切线,求切线方程.
分析 (1)设出抛物线C的方程,利用双曲线的简单性质求出顶点坐标,然后求解抛物线方程.
(2)求出双曲线的左焦点坐标,设出切线方程,联立方程组求解切线方程.
解答 解:(1)依题意,设抛物线C的方程为y2=2px…(1分)
抛物线C的顶点在坐标原点,焦点为双曲线${x^2}-\frac{y^2}{3}=1$的右顶点
$\frac{p}{2}=1$…(2分),
所以p=2,抛物线C的方程为y2=4x…(3分)
(2)双曲线${x^2}-\frac{y^2}{3}=1$的左焦点为F(-2,0)…(4分)
显然x=-2不是抛物线C的切线,设所求切线为y=k(x+2)…(5分)
由$\left\{\begin{array}{l}{y^2}=4x\\ y=k(x+2)\end{array}\right.$及k≠0得,${y^2}=4(\frac{y}{k}-2)$…(6分)
${y^2}-\frac{4}{k}y+8=0$,依题意${(\frac{4}{k})^2}-4×8=0$…(8分),
解得$k=±\frac{{\sqrt{2}}}{2}$…(9分)
切线方程为$y=±\frac{{\sqrt{2}}}{2}(x+2)$…(10分)
点评 本题考查双曲线的简单性质的应用,直线与双曲线的位置关系的应用,考查计算能力.

练习册系列答案
相关题目
20.若关于x,y的不等式组$\left\{\begin{array}{l}{x≤0}\\{x+y≥0}\\{kx-y+1≥0}\end{array}\right.$,表示的平面区域是等腰直角三角形区域,则其表示的区域面积为( )
| A. | $\frac{1}{2}$或$\frac{1}{4}$ | B. | $\frac{1}{2}$或$\frac{1}{8}$ | C. | 1或$\frac{1}{2}$ | D. | 1或$\frac{1}{4}$ |
1.某商场为了解商品销售情况,对某种电器今年一至六月份的月销售量Q(x)(台) 进行统计,得数据如下:
根据如表中的数据,你认为能较好描述月销售量Q(x)(台)与时间x(月份)变化关系的模拟函数是( )
| x(月份) | 1 | 2 | 3 | 4 | 5 | 6 |
| Q(x)(台) | 6 | 9 | 10 | 8 | 6 | 2 |
| A. | Q(x)=ax+b(a≠0) | B. | Q(x)=a|x-4|+b(a≠0) | ||
| C. | Q(x)=a(x-3)2+b(a≠0) | D. | Q(x)=a•bx(a≠0,b>0且b≠1) |
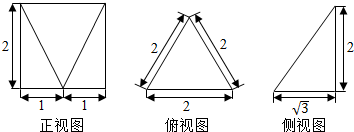
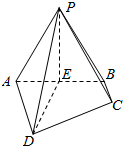 如图,在四棱锥P-ABCD中,AD∥BC,AD⊥平面PAB,△PAB是正三角形,AD=AB=2,BC=1,E是线段AB的中点
如图,在四棱锥P-ABCD中,AD∥BC,AD⊥平面PAB,△PAB是正三角形,AD=AB=2,BC=1,E是线段AB的中点