题目内容
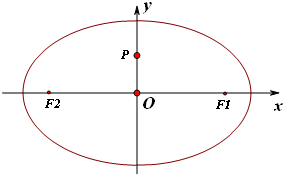 已知椭圆的焦点F1(1,0),F2(-1,0),过P(0,
已知椭圆的焦点F1(1,0),F2(-1,0),过P(0, )作垂直于y轴的直线被椭圆所截线段长为
)作垂直于y轴的直线被椭圆所截线段长为 ,过F1作直线l与椭圆交于A、B两点.
,过F1作直线l与椭圆交于A、B两点.
(1)求椭圆的标准方程;
(2)若A是椭圆与y轴负半轴的交点,求△PAB的面积;
(3)是否存在实数t使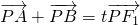 ,若存在,求t的值和直线l的方程;若不存在,说明理由.
,若存在,求t的值和直线l的方程;若不存在,说明理由.
解:(1)设椭圆方程为 (a>b>0),
(a>b>0),
由题意点( ,
, )在椭圆上,a2=b2+1
)在椭圆上,a2=b2+1
∴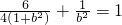 ,∴b2=1,a2=b2+1=2
,∴b2=1,a2=b2+1=2
∴椭圆的标准方程为
(2)由题意,A是椭圆与y轴负半轴的交点,∴A(0,-1)
∵F1(1,0),∴过F1,A作直线l的方程为y=x-1,
代入椭圆方程可得3x2-4x=0
∴x=0或
∴A(0,-1),B( ,
, ),
),
∵P(0, )
)
∴△PAB的面积为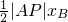 =1
=1
(3)当直线斜率不存在时,可得A(1, ),B(1,-
),B(1,- ),
),
所以 ,
,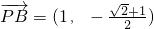 ,
,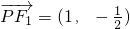
由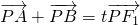 得t=2,直线l的方程为x=1.
得t=2,直线l的方程为x=1.
当直线斜率存在时,设A(x1,y1),B(x2,y2),直线方程为y=k(x-1)
代入椭圆方程可得( +k2)x2-2k2x+k2-1=0
+k2)x2-2k2x+k2-1=0
∴x1+x2=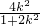
所以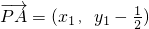 ,
,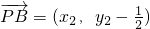 ,
,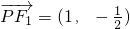
由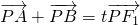 得x1+x2=t,
得x1+x2=t,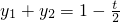
因为y1+y2=k(x1+x2-2),所以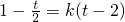
又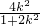 =t,∴k=-
=t,∴k=- ,t=
,t=
此时,直线l的方程为y=- (x-1)
(x-1)
分析:(1)设椭圆的标准方程为 (a>b>0),根据过P(0,
(a>b>0),根据过P(0, )作垂直于y轴的直线被椭圆所截线段长为
)作垂直于y轴的直线被椭圆所截线段长为 ,可得点(
,可得点( ,
, )在椭圆上,,从而可得椭圆的标准方程;
)在椭圆上,,从而可得椭圆的标准方程;
(2)确定过F1,A作直线l的方程代入椭圆方程,求出A,B的坐标,从而可求△PAB的面积;
(3)当直线斜率不存在时,可得A,B的坐标,从而可得向量PA,PB,PF1的坐标,利用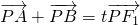 ,即可求得直线l的方程;当直线斜率存在时,确定向量PA,PB,PF1的坐标,利用
,即可求得直线l的方程;当直线斜率存在时,确定向量PA,PB,PF1的坐标,利用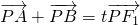 ,即可求得直线l的方程.
,即可求得直线l的方程.
点评:本题考查椭圆的标准方程,考查三角形面积的计算,考查向量知识的运用,考查分类讨论的数学思想,综合性强.
 (a>b>0),
(a>b>0),由题意点(
 ,
, )在椭圆上,a2=b2+1
)在椭圆上,a2=b2+1∴
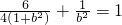 ,∴b2=1,a2=b2+1=2
,∴b2=1,a2=b2+1=2∴椭圆的标准方程为

(2)由题意,A是椭圆与y轴负半轴的交点,∴A(0,-1)
∵F1(1,0),∴过F1,A作直线l的方程为y=x-1,
代入椭圆方程可得3x2-4x=0
∴x=0或

∴A(0,-1),B(
 ,
, ),
),∵P(0,
 )
)∴△PAB的面积为
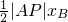 =1
=1(3)当直线斜率不存在时,可得A(1,
 ),B(1,-
),B(1,- ),
),所以
 ,
,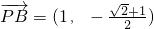 ,
,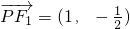
由
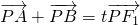 得t=2,直线l的方程为x=1.
得t=2,直线l的方程为x=1.当直线斜率存在时,设A(x1,y1),B(x2,y2),直线方程为y=k(x-1)
代入椭圆方程可得(
 +k2)x2-2k2x+k2-1=0
+k2)x2-2k2x+k2-1=0∴x1+x2=
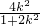
所以
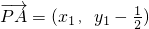 ,
,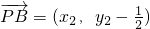 ,
,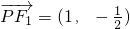
由
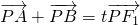 得x1+x2=t,
得x1+x2=t,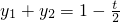
因为y1+y2=k(x1+x2-2),所以
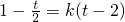
又
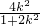 =t,∴k=-
=t,∴k=- ,t=
,t=
此时,直线l的方程为y=-
 (x-1)
(x-1)分析:(1)设椭圆的标准方程为
 (a>b>0),根据过P(0,
(a>b>0),根据过P(0, )作垂直于y轴的直线被椭圆所截线段长为
)作垂直于y轴的直线被椭圆所截线段长为 ,可得点(
,可得点( ,
, )在椭圆上,,从而可得椭圆的标准方程;
)在椭圆上,,从而可得椭圆的标准方程;(2)确定过F1,A作直线l的方程代入椭圆方程,求出A,B的坐标,从而可求△PAB的面积;
(3)当直线斜率不存在时,可得A,B的坐标,从而可得向量PA,PB,PF1的坐标,利用
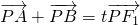 ,即可求得直线l的方程;当直线斜率存在时,确定向量PA,PB,PF1的坐标,利用
,即可求得直线l的方程;当直线斜率存在时,确定向量PA,PB,PF1的坐标,利用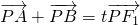 ,即可求得直线l的方程.
,即可求得直线l的方程.点评:本题考查椭圆的标准方程,考查三角形面积的计算,考查向量知识的运用,考查分类讨论的数学思想,综合性强.

练习册系列答案
相关题目
 (2012•宝山区一模)已知椭圆的焦点F1(1,0),F2(-1,0),过P(0,
(2012•宝山区一模)已知椭圆的焦点F1(1,0),F2(-1,0),过P(0,