题目内容
现有某种细胞100个,其中有占总数 的细胞每小时分裂一次,即由1个细胞分裂成2个细胞,按这种规律发展下去,经过多少小时,细胞总数可以超过1010个?(参考数据:lg3=0.477,lg2=0.301).
的细胞每小时分裂一次,即由1个细胞分裂成2个细胞,按这种规律发展下去,经过多少小时,细胞总数可以超过1010个?(参考数据:lg3=0.477,lg2=0.301).
解:现有细胞100个,先考虑经过1、2、3、4个小时后的细胞总数,
1小时后,细胞总数为 +
+ =
= ;
;
2小时后,细胞总数为 =
= ;
;
3小时后,细胞总数为 =
= ;
;
4小时后,细胞总数为 =
= ;
;
可见,细胞总数y与时间x(小时)之间的函数关系为:y=100×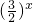 ,x∈N*
,x∈N*
由100×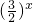 >1010,得
>1010,得 ,两边取以10为底的对数,得xlg
,两边取以10为底的对数,得xlg >8,
>8,
∴x> ,∵
,∵ ,
,
∴x>45.45.
答:经过46小时,细胞总数超过1010个.
分析:由细胞开始时为100个,先考虑经过1、2、3、4个小时后的细胞总数,根据分裂的规律得到细胞总数y与时间x(小时)之间的函数关系为:y=100×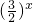 ,x∈N*,再建立不等式求解即可.
,x∈N*,再建立不等式求解即可.
点评:此题考查了函数关系的确定,以及指数函数的实际应用,其中根据题意得出y=100×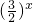 ,x∈N*是解本题的关键.
,x∈N*是解本题的关键.
1小时后,细胞总数为
 +
+ =
= ;
;2小时后,细胞总数为
 =
= ;
;3小时后,细胞总数为
 =
= ;
;4小时后,细胞总数为
 =
= ;
;可见,细胞总数y与时间x(小时)之间的函数关系为:y=100×
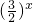 ,x∈N*
,x∈N*由100×
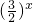 >1010,得
>1010,得 ,两边取以10为底的对数,得xlg
,两边取以10为底的对数,得xlg >8,
>8,∴x>
 ,∵
,∵ ,
,∴x>45.45.
答:经过46小时,细胞总数超过1010个.
分析:由细胞开始时为100个,先考虑经过1、2、3、4个小时后的细胞总数,根据分裂的规律得到细胞总数y与时间x(小时)之间的函数关系为:y=100×
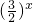 ,x∈N*,再建立不等式求解即可.
,x∈N*,再建立不等式求解即可.点评:此题考查了函数关系的确定,以及指数函数的实际应用,其中根据题意得出y=100×
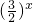 ,x∈N*是解本题的关键.
,x∈N*是解本题的关键. 
练习册系列答案
相关题目
 的细胞每小时分裂一次,即由1个细胞分裂成2个细胞,按这种规律发展下去,经过多少小时,细胞总数可以超过
的细胞每小时分裂一次,即由1个细胞分裂成2个细胞,按这种规律发展下去,经过多少小时,细胞总数可以超过 个?(参考数据:
个?(参考数据: )
) 的细胞每小时分裂一次.即由1个细胞分裂成2个细胞,按这种规律发展下去,经过多少小时,细胞总数可以超过1010个?(精确到小时)(参考数据:lg3≈0.477,lg2≈0.301)
的细胞每小时分裂一次.即由1个细胞分裂成2个细胞,按这种规律发展下去,经过多少小时,细胞总数可以超过1010个?(精确到小时)(参考数据:lg3≈0.477,lg2≈0.301)