题目内容
已知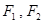 为椭圆
为椭圆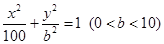 的左、右焦点,
的左、右焦点,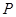 是椭圆上一点,若
是椭圆上一点,若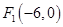 。
。
(1)求椭圆方程;
(2)若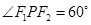 求
求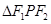 的面积。
的面积。
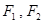 为椭圆
为椭圆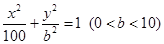 的左、右焦点,
的左、右焦点,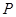 是椭圆上一点,若
是椭圆上一点,若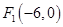 。
。(1)求椭圆方程;
(2)若
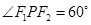 求
求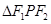 的面积。
的面积。(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)

(2)由已知得

解得
 ,所以
,所以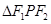 的面积为
的面积为 。考点:
。考点:点评:典型题,涉及椭圆的焦点弦问题,往往要利用椭圆的定义,本题利用椭圆的定义及余弦定理,建立方程组,利用整体代换思想求得
 。
。
练习册系列答案
相关题目
题目内容
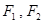 为椭圆
为椭圆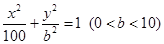 的左、右焦点,
的左、右焦点,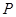 是椭圆上一点,若
是椭圆上一点,若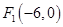 。
。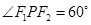 求
求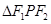 的面积。
的面积。 ;(2)
;(2)


 ,所以
,所以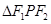 的面积为
的面积为 。考点:
。考点: 。
。