题目内容
已知数列{bn}满足条件:首项b1=1,前n项之和Bn= .
.
(1)求数列{bn}的通项公式;
(2)设数列{an}的满足条件:an=(1+ ) an-1,且a1=2,试比较an与
) an-1,且a1=2,试比较an与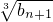 的大小,并证明你的结论.
的大小,并证明你的结论.
解:(1)当n>1时,bn=Bn-Bn-1
= -
-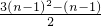 =3n-2
=3n-2
令n=1得b1=1,
∴bn=3n-2.(5分)
(2)由an=(1+ )an-1,得
)an-1,得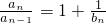
∴an=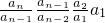
由a1=2,bn=3n-2知,
an=(1+ )(1+
)(1+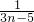 )(1+
)(1+ )2
)2
=(1+1)(1+ )(1+
)(1+ )
)
又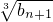 =
=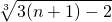 =
=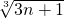 ,(5分)
,(5分)
设cn=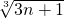 ,
,
当n=1时,有(1+1)=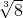 >
>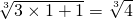
当n=2时,有an=(1+1)(1+ )=
)=
=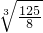 >
>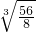 =
=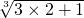 =cn
=cn
假设n=k(k≥1)时an>cn成立,
即(1+1)(1+ )(1+
)(1+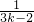 )>
)>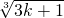 成立,
成立,
则n=k+1时,
左边═(1+1)(1+ )(1+
)(1+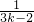 )(1+
)(1+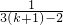 )
)
>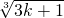 (1+
(1+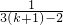 )=
)=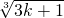
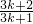 (3分)
(3分)
右边=ck+1=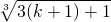 =
=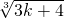
由(ak+1)3-(ck+1)3=(3k+1)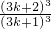 -(3k+4)
-(3k+4)
=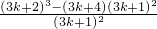
=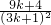 >0,得ak+1>ck+1成立.
>0,得ak+1>ck+1成立.
综合上述,an>cn对任何正整数n都成立.(3分)
分析:(1)由bn=Bn-Bn-1= -
-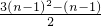 =3n-2,能得到数列{bn}的通项公式.
=3n-2,能得到数列{bn}的通项公式.
(2)由an=(1+ )an-1,得
)an-1,得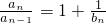 ,an=
,an=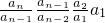 ,由a1=2,bn=3n-2知,an=(1+
,由a1=2,bn=3n-2知,an=(1+ )(1+
)(1+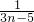 )(1+
)(1+ )2=(1+1)(1+
)2=(1+1)(1+ )(1+
)(1+ ),由此入手,利用数学归纳法能够证明an>
),由此入手,利用数学归纳法能够证明an>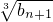 .
.
点评:本题考查数列的性质和应用,解题时要注意数列递推公式的合理运用,合理地运用数学归纳法进行证明.
=
 -
-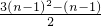 =3n-2
=3n-2令n=1得b1=1,
∴bn=3n-2.(5分)
(2)由an=(1+
 )an-1,得
)an-1,得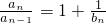
∴an=
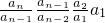
由a1=2,bn=3n-2知,
an=(1+
 )(1+
)(1+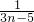 )(1+
)(1+ )2
)2=(1+1)(1+
 )(1+
)(1+ )
)又
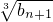 =
=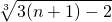 =
=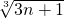 ,(5分)
,(5分)设cn=
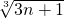 ,
,当n=1时,有(1+1)=
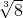 >
>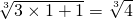
当n=2时,有an=(1+1)(1+
 )=
)=
=
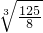 >
>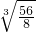 =
=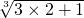 =cn
=cn假设n=k(k≥1)时an>cn成立,
即(1+1)(1+
 )(1+
)(1+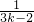 )>
)>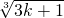 成立,
成立,则n=k+1时,
左边═(1+1)(1+
 )(1+
)(1+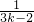 )(1+
)(1+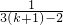 )
)>
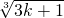 (1+
(1+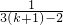 )=
)=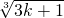
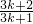 (3分)
(3分)右边=ck+1=
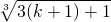 =
=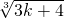
由(ak+1)3-(ck+1)3=(3k+1)
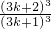 -(3k+4)
-(3k+4)=
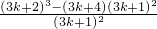
=
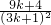 >0,得ak+1>ck+1成立.
>0,得ak+1>ck+1成立.综合上述,an>cn对任何正整数n都成立.(3分)
分析:(1)由bn=Bn-Bn-1=
 -
-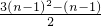 =3n-2,能得到数列{bn}的通项公式.
=3n-2,能得到数列{bn}的通项公式.(2)由an=(1+
 )an-1,得
)an-1,得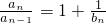 ,an=
,an=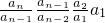 ,由a1=2,bn=3n-2知,an=(1+
,由a1=2,bn=3n-2知,an=(1+ )(1+
)(1+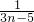 )(1+
)(1+ )2=(1+1)(1+
)2=(1+1)(1+ )(1+
)(1+ ),由此入手,利用数学归纳法能够证明an>
),由此入手,利用数学归纳法能够证明an>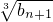 .
.点评:本题考查数列的性质和应用,解题时要注意数列递推公式的合理运用,合理地运用数学归纳法进行证明.

练习册系列答案
相关题目