题目内容
17. 如图,在三棱锥P-ABC中,AB⊥平面PAC,∠APC=90°,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.
如图,在三棱锥P-ABC中,AB⊥平面PAC,∠APC=90°,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.(Ⅰ)证明:平面PCE⊥平面PAB;
(Ⅱ)证明:MN∥平面PAC.
分析 (I)由AB⊥平面PAC可得AB⊥PC,再结合AP⊥PC得出PC⊥平面PAB,故而平面PCE⊥平面PAB;
(II)取AE中点Q,连结NQ,MQ,则可证明平面MNQ∥平面PAC,故而MN∥平面PAC.
解答 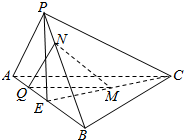 证明:(I)∵AB⊥平面PAC,PC?平面PAC,
证明:(I)∵AB⊥平面PAC,PC?平面PAC,
∴AB⊥PC,
∵∠APC=90°,∴AP⊥PC,
又∵AP?平面PAB,AB?平面PAB,AP∩AB=A,
∴PC⊥平面PAB,∵PC?平面PCE,
∴平面PCE⊥平面PAB.
(II)取AE中点Q,连结NQ,MQ,
∵M是CE中点,∴MQ∥AC,
∵PB=4PN,AB=4AQ,
∴QN∥AP,
又∵AP∩PC=P,AP?平面APC,PC?平面APC,QN∩QM=Q,QN?平面MNQ,QM?平面MNQ,
∴平面MNQ∥平面PAC,
∵MN?平面MNQ,
∴MN∥平面PAC.
点评 本题考查了面面垂直的判定,线面平行的判定,构造平行平面是常用解题方法之一.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
5.定义在(-1,1]的函数f(x)满足f(x)+1=$\frac{1}{f(x+1)}$,且当x∈[0,1]时,f(x)=-x,若g(x)=f(x)+kx+k有一个零点,则实数k的取值范围是( )
| A. | [2,+∞) | B. | [0,$\frac{1}{2}$]∪(2,+∞) | C. | (-$\frac{1}{2}$,+∞) | D. | [-$\frac{1}{2}$,0]∪[2,+∞) |
12.设函数f(x)满足x3f′(x)+3x2f(x)=1+lnx,且f($\sqrt{e}$)=$\frac{1}{2e}$,则x>0时,f(x)( )
| A. | 有极大值,无极小值 | B. | 有极小值,无极大值 | ||
| C. | 既有极大值又有极小值 | D. | 既无极大值也无极小值 |
6.若ω≠0,函数f(x)=$\frac{tanωx-\sqrt{3}}{\frac{\sqrt{3}}{3}+tanωx}$图象的相邻两个对称中心之间的距离是$\frac{π}{2}$,则ω的值是( )
| A. | $\frac{π}{2}$ | B. | ±2 | C. | 2 | D. | ±1 |