题目内容
已知△ABC的三个内角A，B，C所对的边分别为a，b，c，A是锐角，且
b＝2a·sin B.
(1)求A；
(2)若a＝7，△ABC的面积为10，求b2＋c2的值．
解 (1)∵b＝2a·sin B，由正弦定理知
sin B＝2sin A·sin B.
∵B是三角形的内角，∴sin B>0，从而有sin A＝
，
∴A＝60°或120°，∵A是锐角，∴A＝60°.
(2)∵10＝
bcsin 
，∴bc＝40，
又72＝b2＋c2－2bccos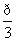 
，∴b2＋c2＝89.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
＝8，
＝5，则
的取值范围是__________．
，b＝
，则A＝________.
os2x
＝_______
_.
)
变换过程．
，则p是q的