题目内容
已知函数f(x)=loga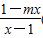 (a>0且a≠1)是奇函数.
(a>0且a≠1)是奇函数.
(1)求m的值;
(2)判断f(x)在区间(1,+∞)上的单调性并加以证明;
(3)当a>1,x∈(1,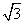 )时,f(x)的值域是(1,+∞),求a的值.
)时,f(x)的值域是(1,+∞),求a的值.
(1)∵f(x)是奇函数,x=1不在f(x)的定义域内,∴x=-1也不在函数定义域内,
令1-m·(-1)=0得m=-1.
(也可以由f(-x)=-f(x)恒成立求m)
(2)由(1)得f(x)=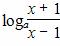 (a>0且a≠1),
(a>0且a≠1),
任取x1、x2∈(1,+∞),且x1<x2,
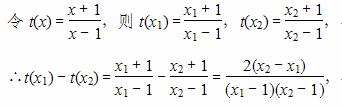 ∵x1>1,x2>1,x1<x2,
∵x1>1,x2>1,x1<x2,
∴x1-1>0,x2-1>0,x2-x1>0.
∴t(x1)>t(x2),即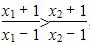
∴当a>1时,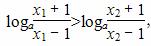
即f(x1)>f(x2);
当0<a<1时,
即f(x1)<f(x2),
∴当a>1时,f(x)在(1,+∞)上是减函数,当0<a<1时,f(x)在(1,+∞)上是增函数.
(3)∵a>1,∴f(x)在(1,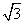 )上是减函数,
)上是减函数,
∴当x∈(1,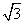 )时,f(x)>f(
)时,f(x)>f(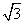 )=loga(2+
)=loga(2+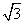 ),
),
由条件知,loga(2+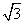 )=1,∴a=2+
)=1,∴a=2+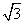 .
.

练习册系列答案
相关题目
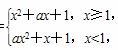 则“-2≤a≤0”是“函数f(x)在R上单调递增”的( )
则“-2≤a≤0”是“函数f(x)在R上单调递增”的( )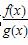 <0的解集是________.
<0的解集是________.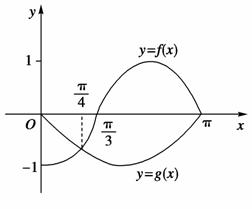
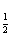 3),c=f(0.20.6),则a、b、c的大小关系是( )
3),c=f(0.20.6),则a、b、c的大小关系是( )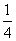 ),则f(x)的一个递减区间是( )
),则f(x)的一个递减区间是( ) ,c=(
,c=(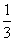 )
) ,则( )
,则( ) |与y=-
|与y=- 在同一平面直角坐标系内的大致图象为( )
在同一平面直角坐标系内的大致图象为( )