题目内容
15.在△ABC中,$\overrightarrow{AP}$=$\frac{1}{6}$$\overrightarrow{AB}$+$\frac{2}{5}$$\overrightarrow{AC}$,则S△APB:S△CPB=12:13.分析 可过PAC∥PD,PE∥AB,分别交AB,AC于D,E,则得到四边形ADPE为平行四边形,从而可以得出$\overrightarrow{AD}=\frac{1}{6}\overrightarrow{AB},\overrightarrow{AE}=\frac{2}{5}\overrightarrow{AC}$,从而有DP∥AC,且$DP=\frac{2}{5}AC$,PE∥AB,且$PE=\frac{1}{6}AB$,从而可得到${S}_{△APB}=\frac{2}{5}{S}_{△ABC},{S}_{△APC}=\frac{1}{6}{S}_{△ABC}$,${S}_{△CPB}=\frac{13}{30}{S}_{△ABC}$,这样便可得出S△APB:S△CPB的值.
解答  解:如图,过P作AC∥PD,交AB于D,作PE∥AB,交AC于E,则:
解:如图,过P作AC∥PD,交AB于D,作PE∥AB,交AC于E,则:
四边形ADPE为平行四边形,$\overrightarrow{AP}=\overrightarrow{AD}+\overrightarrow{AE}$;
∴$\overrightarrow{AD}=\frac{1}{6}\overrightarrow{AB},\overrightarrow{AE}=\frac{2}{5}\overrightarrow{AC}$;
∴$DP=\frac{2}{5}AC,PE=\frac{1}{6}AB$;
∴${S}_{△APB}=\frac{2}{5}{S}_{△ABC},{S}_{△APC}=\frac{1}{6}{S}_{△ABC}$;
∴${S}_{△CPB}=\frac{13}{30}{S}_{△ABC}$;
∴S△APB:S△CPB=12:13.
故答案为:12:13.
点评 考查向量加法的平行四边形法则,平面向量基本定理,向量数乘的几何意义,以及三角形的面积公式.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | 3 | B. | 1 | C. | 0 | D. | -1 |
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
 是曲线
是曲线 的切线,也是曲线
的切线,也是曲线 的切线,则
的切线,则 _________.
_________.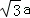 =2csinA
=2csinA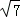 ,且△ABC的面积为
,且△ABC的面积为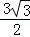 ,求a+b的值
,求a+b的值