题目内容
已知函数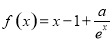 (
(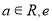 为自然对数的底数).
为自然对数的底数).
(1)若曲线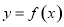 在点
在点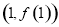 处的切线平行于
处的切线平行于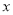 轴,求
轴,求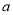 的值;
的值;
(2)讨论函数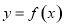 的极值情况;
的极值情况;
(3)当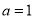 时,若直线
时,若直线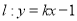 与曲线
与曲线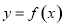 没有公共点,求k的取值范围.
没有公共点,求k的取值范围.
(1)a=e; (2)当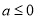 时,
时,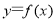 无极值;当
无极值;当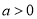 时,
时,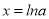 ;(3)k≤1.
;(3)k≤1.
【解析】
试题分析:(1)由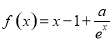 ,得
,得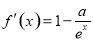 ,
,
又曲线y=f(x)在点(1,f(1))处的切线平行于x轴,
∴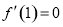 ,即
,即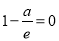 ,解得a=e.
,解得a=e.
(2) 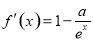 .
.
①当a≤0时,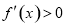 ,f(x)为(-∞,+∞)上的增函数,所以f(x)无极值;
,f(x)为(-∞,+∞)上的增函数,所以f(x)无极值;
②当a>0时,令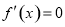 ,得
,得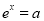 ,
,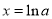 ,
,
x∈(-∞,lna),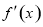 <0;x∈(lna,+∞),
<0;x∈(lna,+∞),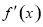 >0;
>0;
∴f(x)在∈(-∞,lna)上单调递减,在(lna,+∞)上单调递增,
故f(x)在x=lna处取到极小值,且极小值为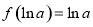 ,无极大值.
,无极大值.
综上,当a≤0时,f(x)无极值;当a>0时,f(x)在x=lna处取到极小值lna,无极大值.
(3)当a=1时,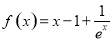 ,令
,令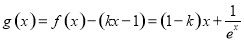 ,
,
则直线l:y=kx-1与曲线y=f(x)没有公共点,
等价于方程g(x)=0在R上没有实数解.
假设k>1,此时g(0)=1>0, ,
,
又函数g(x)的图象连续不断,由零点存在定理可知g(x)=0在R上至少有一解,与“方程g(x)=0在R上没有实数解”矛盾,故k≤1.
又k=1时,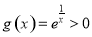 ,知方程g(x)=0在R上没有实数解,
,知方程g(x)=0在R上没有实数解,
所以k的取值范围是k≤1.
考点:考查了导数的几何意义,利用导数研究函数的极值和零点的存在性定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
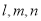 是三条不同的直线,
是三条不同的直线,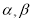 是两个不同的平面,下列命题为真命题的是 ( )
是两个不同的平面,下列命题为真命题的是 ( )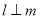 ,
,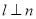 ,
,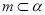 ,
,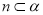 ,则
,则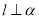 ,
,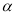 ∥
∥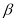 ,
, ,则
,则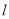 ∥
∥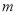 ,
,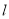 ∥
∥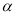
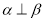 ,
,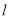 ∥
∥
 在区间
在区间 内可导,且
内可导,且 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 的所有切线中,斜率最小的切线方程是 .
的所有切线中,斜率最小的切线方程是 . 的零点所在区间为( )
的零点所在区间为( ) B.
B. C.
C. D.
D.
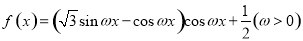 的周期为
的周期为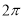 .
.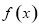 的解析式;
的解析式;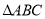 中,角A、B、C的对边分别是
中,角A、B、C的对边分别是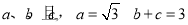 ,
,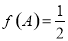 ,求
,求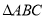 的面积.
的面积. 的图象是
的图象是
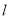 的对称点为B(7,-4),则直线
的对称点为B(7,-4),则直线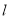 的方程是________.
的方程是________.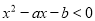 的解集为{x|2<x<3},则a+b=________.
的解集为{x|2<x<3},则a+b=________.