题目内容
设函数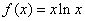
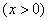 .
.
(Ⅰ) 求函数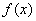 的最小值;
的最小值;
(Ⅱ) 设
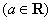 ,讨论函数
,讨论函数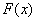 的单调性;
的单调性;
(Ⅲ)斜率为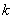 的直线与曲线
的直线与曲线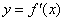 交于
交于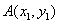 、
、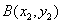
 两点,
两点,
求证: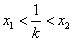 .
.
(Ⅰ) 解:
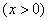 ,令
,令 ,得
,得 .
.
∵当 时,
时, ;当
;当 时,
时, ,
,
∴当 时,
时, .
.
(Ⅱ)
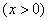 ,
, .
.
① 当 时,恒有
时,恒有 ,
,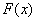 在
在 上是增函数;
上是增函数;
② 当 时,令
时,令 ,得
,得 ,解得
,解得 ;
;
令 ,得
,得 ,解得
,解得 .
.
综上,当 时,
时,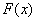 在
在 上是增函数;
上是增函数;
当 时,
时,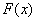 在
在 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
(Ⅲ) 证: .
.
要证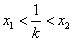 ,即证
,即证 ,等价于证
,等价于证 ,令
,令 ,
,
则只要证 ,由
,由 知
知 ,故等价于证
,故等价于证 (*).
(*).
① 设 ,则
,则 ,故
,故 在
在 上是增函数,
上是增函数,
∴ 当 时,
时, ,即
,即 .
.
② 设 ,则
,则 ,故
,故 在
在 上是增函数,
上是增函数,
∴ 当 时,
时, ,即
,即 .
.
由①②知(*)成立,得证.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 ,则
,则 在复平面上对应的点位于第 象限
在复平面上对应的点位于第 象限 成等比数列,则函数
成等比数列,则函数 的图象与x轴交点的个数是______个.
的图象与x轴交点的个数是______个. 内的任意
内的任意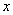 都有
都有 ,且当
,且当 时其导函数
时其导函数 满足
满足 若
若 则( )
则( ) B.
B.
 D.
D.
 。
。 的最小值和最小正周期;
的最小值和最小正周期; 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 sinB-2sinA=0,
sinB-2sinA=0, 。
。 的图象,只需将函数
的图象,只需将函数 的图象 ( )
的图象 ( ) 个单位 B.向左平移
个单位 B.向左平移 个单位
个单位  个单位
个单位 ,向量
,向量 ,且
,且 与
与 的夹角为
的夹角为 ,则
,则 在
在 方向上的投影是____
方向上的投影是____ 与双曲线
与双曲线 的右支交于不同的两点,那么
的右支交于不同的两点,那么 的取值范围是 ( )
的取值范围是 ( ) ) B.(
) B.( ) C.(
) C.( ) D.(
) D.( )
)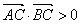 ; 条件乙:点C的坐标是方程
; 条件乙:点C的坐标是方程 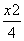 +
+ 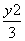 = 1 (y¹0)的解. 则甲是乙的( )
= 1 (y¹0)的解. 则甲是乙的( )