题目内容
1．已知复数z满足：z（1-i）=2+4i，其中i为虚数单位，则复数z的模为$\sqrt{10}$．分析 把已知的等式变形，利用复数代数形式的乘除运算化简，代入模的公式得答案．
解答 解：由z（1-i）=2+4i，得
$z=\frac{2+4i}{1-i}=\frac{（2+4i）（1+i）}{（1-i）（1+i）}=\frac{-2+6i}{2}=-1+3i$，
∴$|z|=\sqrt{（-1）^{2}+{3}^{2}}=\sqrt{10}$．
故答案为：$\sqrt{10}$．
点评 本题考查复数代数形式的乘除运算，考查了复数模的求法，是基础的计算题．
练习册系列答案
名校课堂系列答案
相关题目
11．
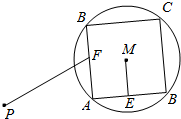如图，已知圆M的半径为2，点P与圆心M的距离为4，正方形ABCD是圆M的内接四边形，E，F是边AB，AD的中点，当正方形ABCD绕圆心M转动时，$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是（ ）
如图，已知圆M的半径为2，点P与圆心M的距离为4，正方形ABCD是圆M的内接四边形，E，F是边AB，AD的中点，当正方形ABCD绕圆心M转动时，$\overrightarrow{PF}$•$\overrightarrow{ME}$的取值范围是（ ）| A． | [-2，2] | B． | [-2$\sqrt{2}$，2$\sqrt{2}$] | C． | [-4，4] | D． | [-4$\sqrt{2}$，4$\sqrt{2}$] |
12．下列命题中，真命题是（ ）
| A． | ?x0∈R，ex＜0 | |
| B． | 若a，b∈R，a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| C． | 命题p：?x∈R，f（x）≥0，则?p：?x0∈R，f（x）＜0 | |
| D． | 命题“在△ABC中，若$\overrightarrow{AB}•\overrightarrow{BC}$＜0，则△ABC为钝角三角形的逆命题为真命题 |
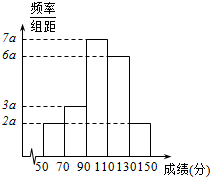贵阳市某数学教师从他所教的2015届高三（X）班与高三（Y）班学生的高考数学成绩中，随机抽取20名学生的成绩绘制成频率分布直方图，如图所示．