题目内容
11.求证:函数f(x)=x-$\frac{1}{x}$,x∈(-∞,0)是增函数.分析 利用取值、作差、变形、判断符号、下结论这五步进行证明,主要利用通分和提取公因式进行变形.
解答 设任意的x1,x2∈(-∞,0),且x1<x2,
则f(x1)-f(x2)
=(x1-$\frac{1}{{x}_{1}}$)-(x2-$\frac{1}{{x}_{2}}$)
=(x1-x2)+($\frac{1}{{x}_{2}}$-$\frac{1}{{x}_{1}}$)
=(x1-x2)+$\frac{{x}_{1}{-x}_{2}}{{{x}_{1}x}_{2}}$
=(x1-x2)(1+$\frac{1}{{{x}_{1}x}_{2}}$)
=(x1-x2)•$\frac{{{x}_{1}x}_{2}+1}{{{x}_{1}x}_{2}}$,
∵x1<0,x2<0,且x1<x2,
∴x1-x2<0,x1x2>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴f(x)在(-∞,0)上是增函数.
点评 本题主要考查函数单调性的判断和证明,利用定义法和导数法是解决函数单调性的基本方法.要求熟练掌握常见证明函数单调性的方法.属于基础题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
16.已知球O的直径长为12,当它的内接正四棱锥的体积最大时,该四棱锥的底面边长为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
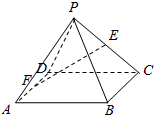 如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.
如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.