题目内容
18.正项等比数列{an}满足a1=1,a2a6+a3a5=128,则下列结论正确的是( )| A. | ?n∈N*,anan+1≤an+2 | B. | ?n∈N*,an+an+2=2an+1 | ||
| C. | ?n∈N*,Sn<an+1 | D. | ?n∈N*,an+an+3=an+1+an+2 |
分析 根据题意先求出q,求出通项公式,再分别判断即可.
解答 解:设公比为q,正项等比数列{an}满足a1=1,a2a6+a3a5=128,
∴q6+q6=128,
∴q6=64=26,解得q=2,
∴an=2n-1,
∴an+1=2n,an+2=2n+1,
若anan+1≤an+2,
∴22n-1≤2n+1,
∴2n-1≤n+1,
解得n≤2,故A不正确,
若an+an+2=2an+1,
∴2n-1+2n+1=2•2n,
则1+4=2×2,
显然不成立,故B不正确,
∵Sn=$\frac{1-{2}^{n}}{1-2}$=2n-1,
若Sn<an+1,
∴2n-1<2n,恒成立,故C正确,
∵an+3=2n+2,
若an+an+3=an+1+an+2,
∴2n-1+2n+2=2n+2n+1,
即1+8=2+4,
显然不成立,故D不正确,
故选:C.
点评 本题考查了等比数列的通项公式和等比数列的前n项和公式,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
8.已知△ABC中,AC=2,AB=4,AC⊥BC,点P满足$\overrightarrow{AP}$=x$\overrightarrow{AC}$+y$\overrightarrow{AB}$,x+2y=1,则$\overrightarrow{PA}$•($\overrightarrow{PB}$+$\overrightarrow{PC}$)的最小值等于( )
| A. | -2 | B. | -$\frac{28}{9}$ | C. | -$\frac{25}{8}$ | D. | -$\frac{7}{2}$ |
9.设m∈R,函数f(x)=(x-m)2+(e2x-2m)2,若存在x0使得f(x0)≤$\frac{1}{5}$成立,则m=( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
6.设a,b,c为三条不同的直线,α,β是两个不同的平面,则下列判断正确的是( )
| A. | 若a⊥b,b⊥c,则a⊥c | B. | 若a∥α,b∥α,则a∥b | C. | 若a∥α,b⊥α,则b∥α | D. | 若a⊥α,α∥β,则a⊥β |
10.若△ABC的面积为64,边AB与AC的等比中项为12,则sinA=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{8}{9}$ |
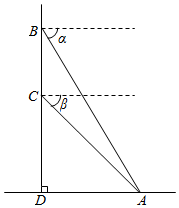 如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).
如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).