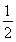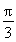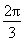Question

在△ABC中,内角A,B,C的对边分别是a,b,c,且a²=b²+c²+bc.

(1)求A.

(2)设a=,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的值.

Answer 1

【解析】(1)由余弦定理得cosA===-.

又因0<A<π,所以A=.

(2)由(1)得sinA=,又由正弦定理及a=得

S=bcsinA=··asinC=3sinBsinC,

因此,S+3cosBcosC=3(sinBsinC+cosBcosC)=3cos(B-C).

所以,当B=C,即B==时,S+3cosBcosC取得最大值3.