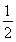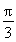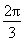Question

在△ABC中内角∠A，∠B所对的边为a，b，已知∠A=45 °，a=

6

，b=3，则∠B=

 

Answer 1

分析：利用正弦定理可题设中a，b和A的值求得sinB的值，进而根据B的范围求得B．

解答：解：由正弦定理可知：

a

sinA

=

b

sinB

∴sinB=

2 2

6

×3=

3

2

∵0＜B＜180°
∴B=60°或120°
故答案为：60°或120°

点评：本题主要考查了正弦定理的应用．考查了学生对三角函数基础知识的掌握，属基础题．