Question

（2012年高考（浙江理））在ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=,sinB=cosC.

(Ⅰ)求tanC的值;

(Ⅱ)若a=,求ABC的面积.

Answer 1

【解析】本题主要考察三角恒等变换,正弦定理,余弦定理及三角形面积求法等知识点.

(Ⅰ) ∵cosA=>0,∴sinA=,

又cosC=sinB=sin(A+C)=sinAcosC+sinCcosA

=cosC+sinC.

整理得:tanC=.

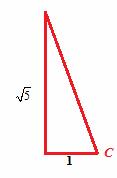
(Ⅱ)由图辅助三角形知:sinC=.

又由正弦定理知:,

故. (1)

对角A运用余弦定理:cosA=. (2)

解(1) (2)得: or  b=(舍去).

∴ABC的面积为:S=.

【答案】(Ⅰ) ;(Ⅱ) .